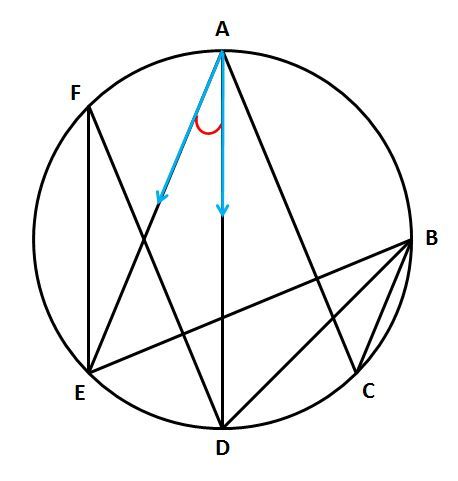
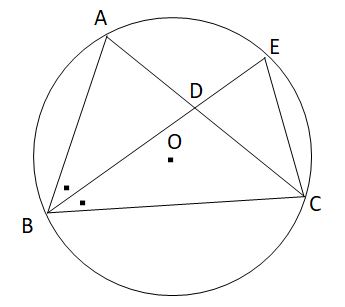
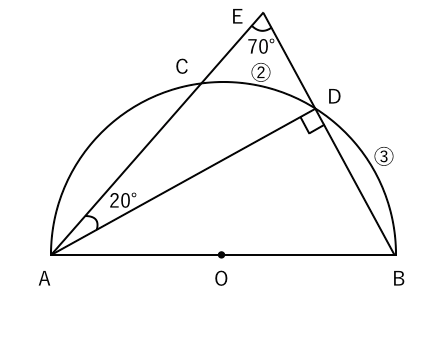
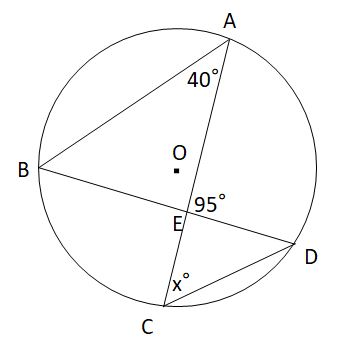
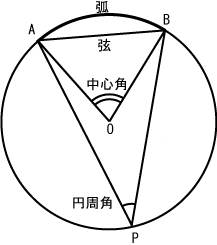
X ①の解説 ②③④⑤⑨の解説 ⑥⑧の解説 ⑦の解説 ⑩の解説 ⑪の解説 ⑫の解説円周角5(発展) acは円oの直径、 ∠acb=70°のとき、 ∠fecを求めよ。 練習問題は印刷してプリントとして使えるものから、pcやスマホから直接できるものまであり、普段の予習復習や定期テスト対策、受験勉強まで中学生の学習を強力にサポートします。円周角の定理に関する問題の解説お願いします。 月曜日に数学のテストがありますが, 対策プリントの円周角の問題が分からずに困っています。(解答ももらってません) ∠xの大きさを求められる方,解説お願いします。
高校入試 英語 数学 円 重要問題
円周角 問題 わからない
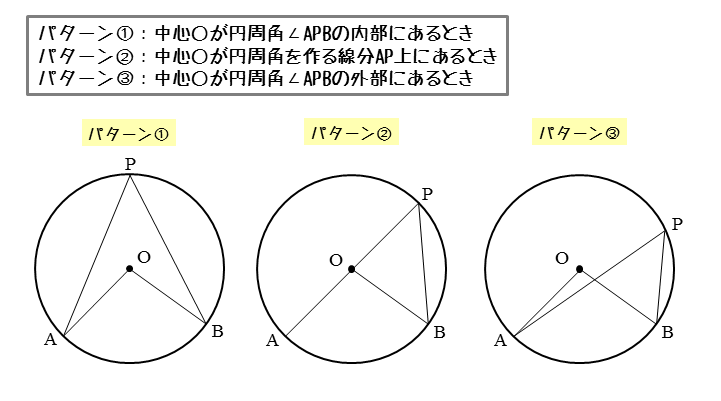
円周角 問題 わからない-点 を弦 について点 と同じ側にあるとき, 以下の内容を証明せよ。 (1) 点 が円の内部にあるとき, (2) 点 が円周上にあるとき, (3) 点 が円の外部にあるとき, 練習問題 解答へ 平面図形 円の性質 円周角 例題 練習問題円周=直径×円周率 円周=半径×2×円周率 となります。 小学校では、円周率を314として計算します。 *公式を理解すれば、基本問題はそれほど難しくないと思います。計算ミスをしないよう314をかけるかけ算をたくさん練習しましょう。 練習問題を
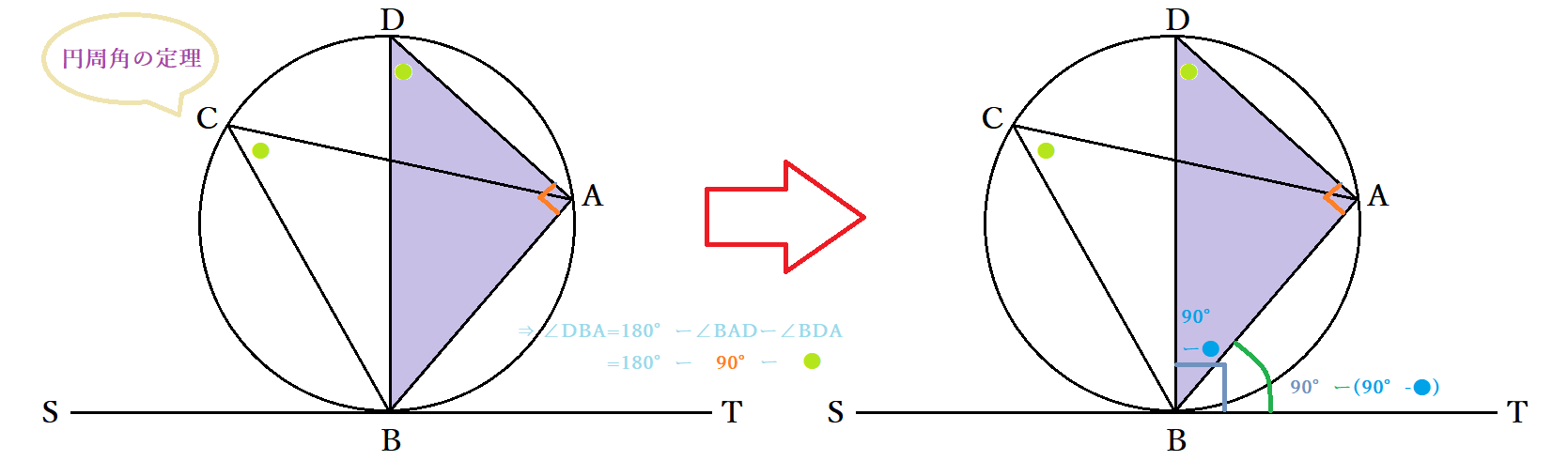



接弦定理とは 接線と弦の作る角の定理の証明 覚え方と応用問題 中学 高校 Curlpingの幸せblog
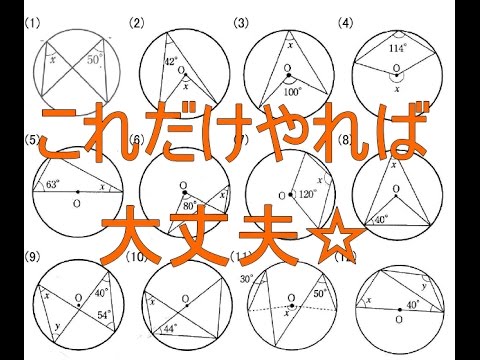
弧bcに円周角を考えると円周角は中心角の半分のため∠bac=44度。 今問題文の条件から⊿abcは二等辺三角形のため底角は等しい。つまり∠abc=∠acb=(180-44)/2=68度 求めたいと思っていた∠bcd=∠acb=68度 ⊿bdcに注目すると∠bdc=180-68-46=66度となる。定理 1 : 1 つの弧に対する円周角は中心角の半分 定理 2 : 1 つの弧に対する円周角はすべて等しい ∠ A Q B = ∠ A P B = ∠ A R B (すべて AB ⌢ に対する円周角) 1:10 例題 10 選 (1) 対頂角は等しい (紫の角) 1 つの弧 (オレンジ色)に対する円周角は等しいX x O 132°
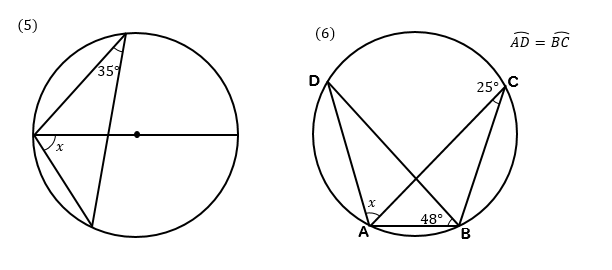
円周角の定理を使った練習問題です。ここで差がつく! 円周角の定理がさまざまあるので、問題文からキーワードを読み取り、定理・性質を活用して解きましょう。 キーワードになりえるもの直径、内接する四角形、弧の比、共通する弧など 今回使う公式(円円周角の問題まとめ 問題演習お疲れ様でした。 円周角の問題を解いていくために大切な問題をパターン別に解説していきました。 今回解いてもらった問題を全て理解することができるれば 他の問題に⑤ ⑥ 1 2 48 1 105 114 NO 1 /8点 x o o x
問題 (ラングレーの問題) 凸四角形abcdにおいて, ∠abd=°, ∠dbc=60°, ∠bca=50°, ∠acd=30°のとき, ∠bdaを求め,その角度となることを初等幾何で証明してください.円周角の定理の逆とは? 次に、「円周角の定理の逆」について説明します。 逆って何?と思った方もいるでしょう。「円周角の定理の逆」とは、 図で表すと、以下のときは、 a,b,p,qが円周上にある、ということです。 なぜこうなるのか説明する前に、Title FdData中間期末過去問題中学数学3年(円周角と中心角/円周角の定理/接線) Author Fd教材開発 Created Date
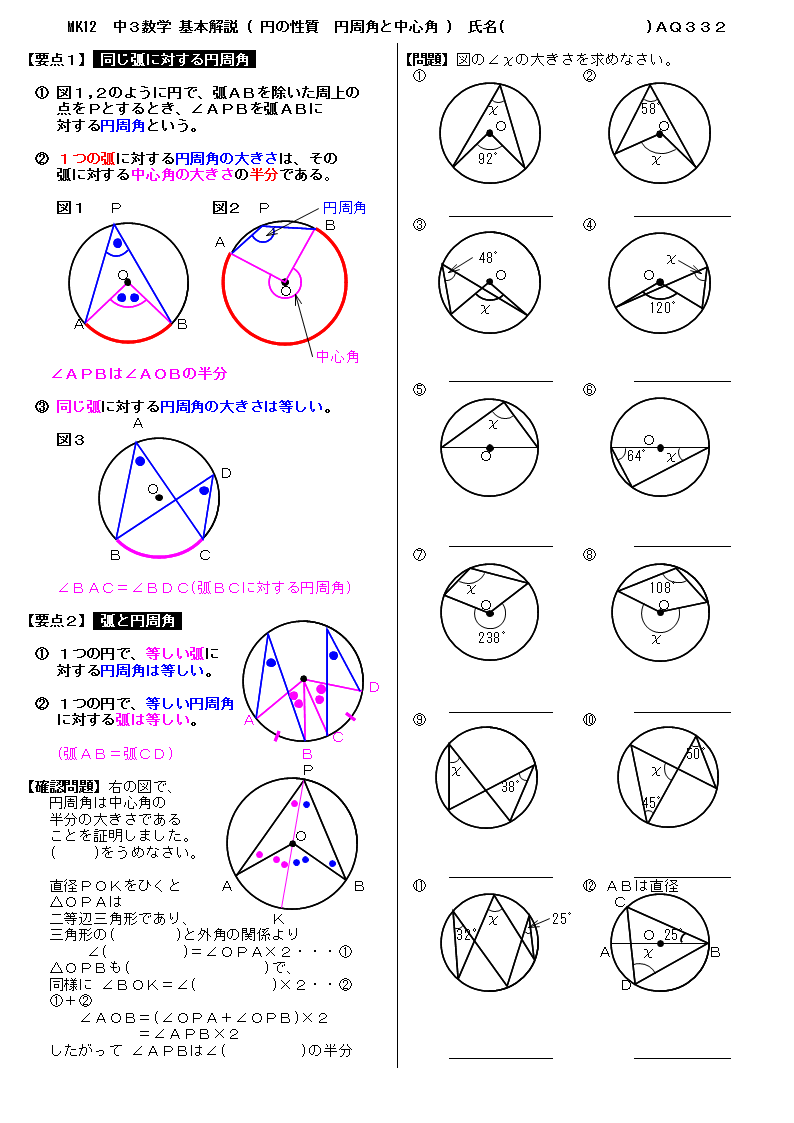



無料 中3数学 基本解説 問題プリント 332 円の性質 円周角と中心角



1
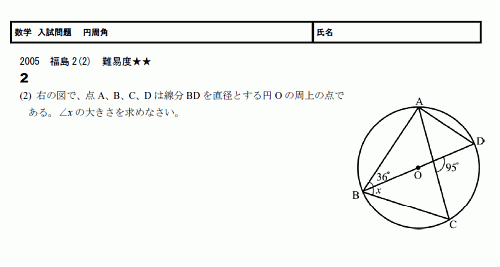
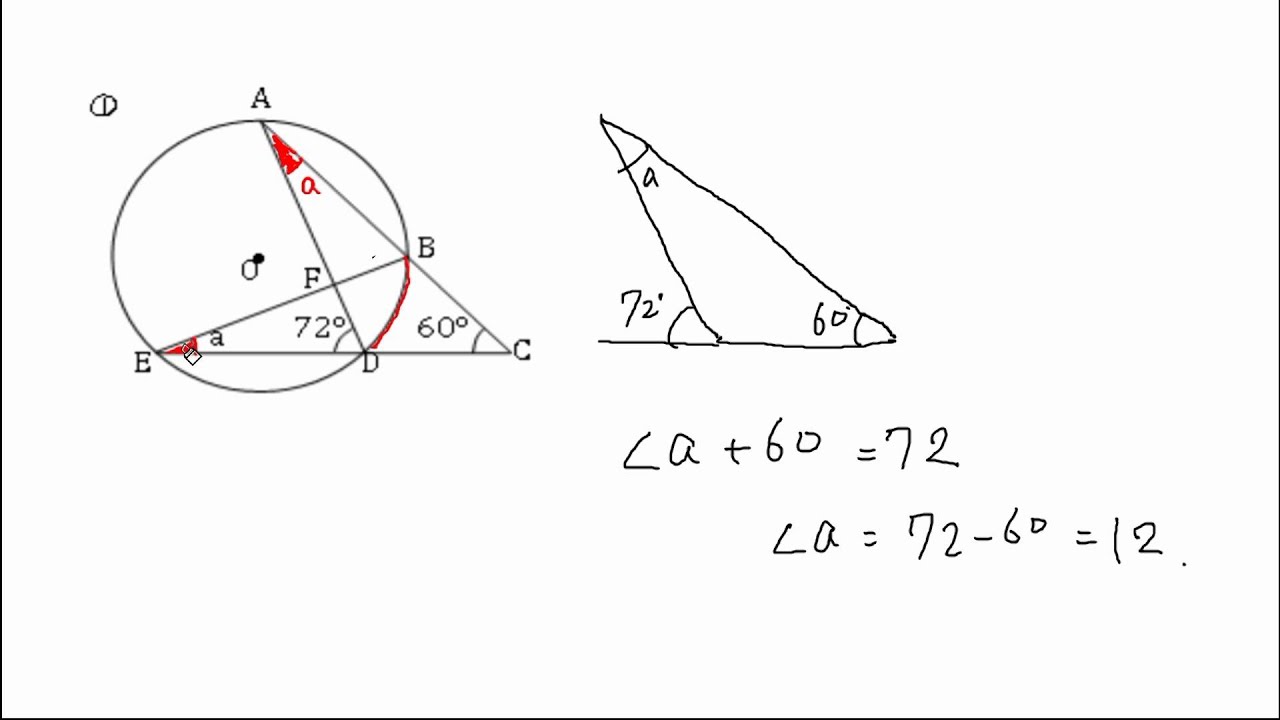
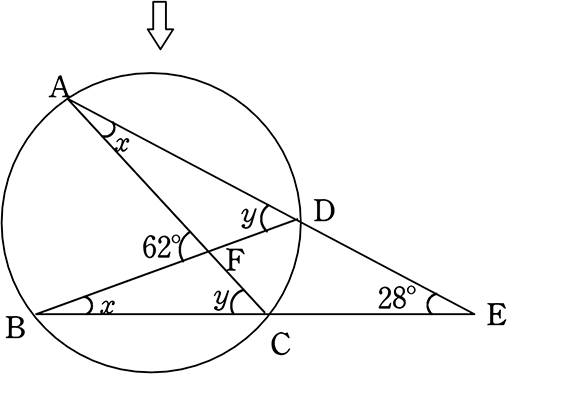
一般に,高校入試問題では「円周角の定理」を覚えているだけでは,問題は解けません.この問題では,次の2つの定理を組み合わせて解いています. (1) 二等辺三角形の2つの底角は等しい. (2) 円周角は中心角の半分になる.こんにちは!レオンです。 今回はこの問題を解いていこうと思います(*´ω`*) 19年の大阪教育大学附属高等学校平野校舎の過去問より。 円周角の定理を使った良い問題だと思います。 持っている知識を生かして柔軟に考えてみて下さい! ヒント 答え 詳しい解説 ① 状況把握 ②X O x 28°



円周角 スタディーx




接弦定理とは 接線と弦の作る角の定理の証明 覚え方と応用問題 中学 高校 Curlpingの幸せblog
X O O x 128°円周角ときたら、対になるもの、中心角です。 円周角が \(30°\) なのですから、中心角は \(60°\) です。 これって・・・正三角形の作図です! 以上、作図方法が見えましたね。 あとは手順にしたがって作図を進めていくのみです。円周角の問題を解くコツ についてまとめます。 3つのポイントに 注意して問題に取り組むこと。 1.弧に注目する 2.直径が出てきたら 90°の円周角を探す 3.補助線を引いてみる 「できる」と自分を信じて




円周角の定理の逆をつかった問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく



これで大丈夫 高校入試 円周角の必勝法 高校入試徹底対策ガイド
円周角の定理が使えると、対頂角と合わせることで、簡単に相似は証明できます。 実際の出され方 実際は図形が複雑化します。 使わない余計な線を増やしたり、三角形の数を増やしたりして、分かりにくくされて出題されます。 当日図形問題が分から円周角 補助線を引く問題 円周角の定理 1つの弧に対する円周角の大きさは一定であり、 その弧に対する中心角の半分である。 2つの半径OA, OBと弦ABによって できる三角形は必ず二等辺三角形になる。 A B O 中心Oに向かって補助線をひき、二等辺三角形やX O O 62°
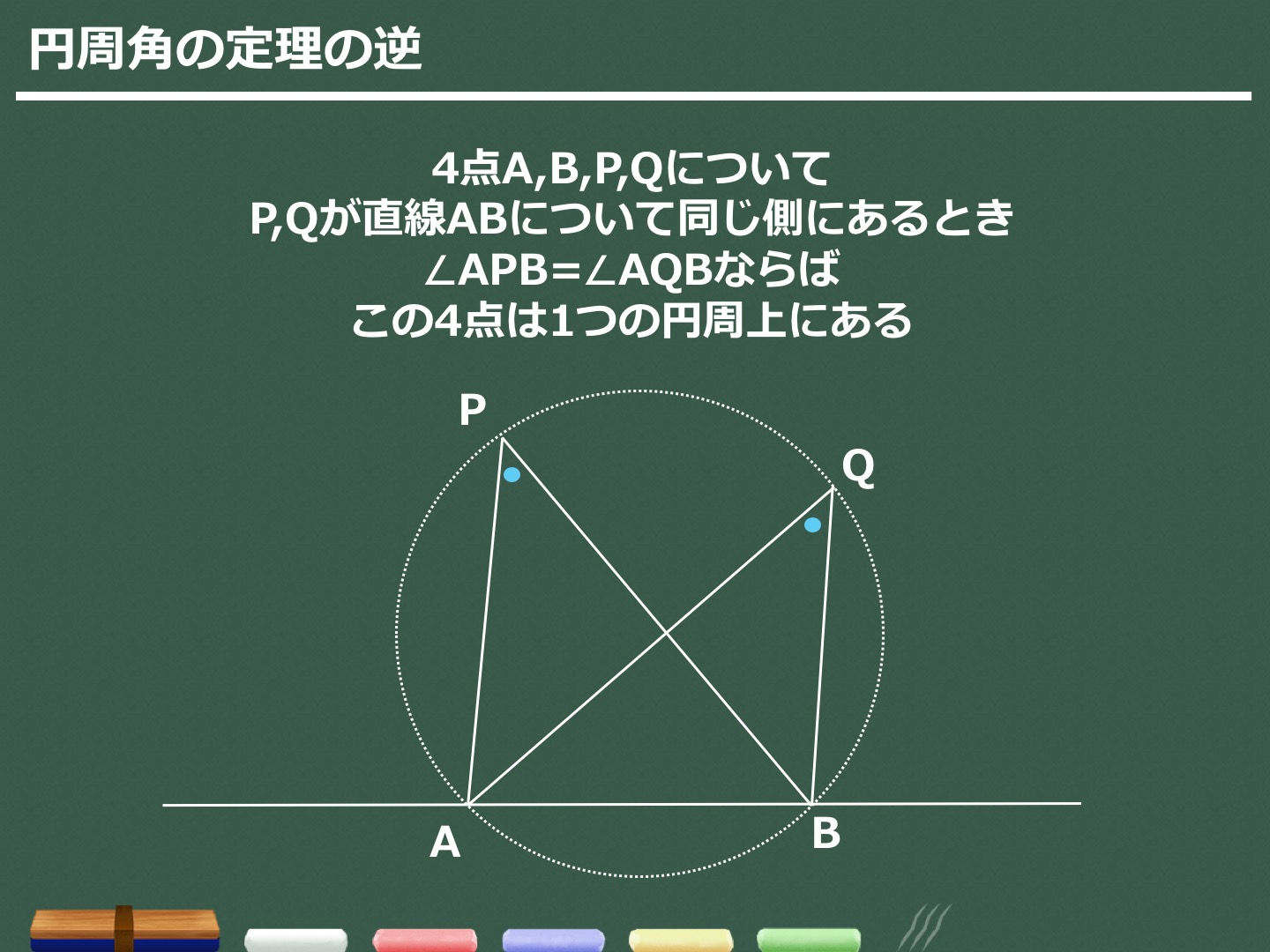



3分でわかる 円周角の定理とその逆の証明 問題の解き方 合格サプリ




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく
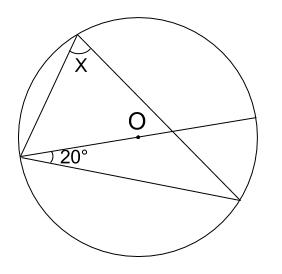
円周角1 それぞれのxの値を求めよ。 ただし、点Oは円の中心である。 78°数学 高校入試問題 円周角 05岩手県4 難易度★★★(pdf) 円周角の問題です。 うちの塾では、角度を求める問題(求角問題と言うようです。)はとても盛り上がりました。 むずかしめの問題を5問くらい並べたプリントを用意して、みんなに渡します。解説 ∠ x =∠boc=∠bac×2=40




世界一わかりやすい数学問題集中3 6章 円の性質




数学 中3 57 円周角の定理 少し応用編 Youtube
円周角と中心角の関係や、それを証明する方法を理解し、円周角の定理を活用する問題を繰り返し練習します。 円周角の定理(1) ⇒ 答え 円周角の定理(2) ⇒ 答え ⇒ 大問1の (2)の「円に内接する四角形の性質」を用いた場合の解説はこちら 円周角の円周角の定理の利用 \(45°\) は \(90°\) の半分なので、以下のような円がかければ 点 \(p\) がとれます。 円周角と中心角の関係ですね。 ※図はラフスケッチであり、不正確です。 この円を目標にします。 三角形 \(oab\) が直角二等辺三角形なので、円周角の定理に関する基本的な問題です。基本事項下の図のように 一つの孤に対する「円周角」の大きさは,「中心角」の半分になります. 同じ弧に対する円周角は等しくなります。覚えるのはこの2点だけです。 このような形になっている場合も円周角は中心角の半分になります。




円周角 Traola Twitterren
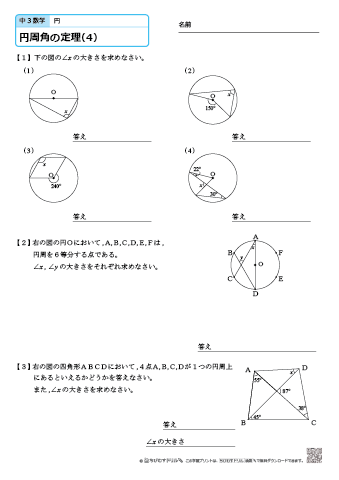



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生
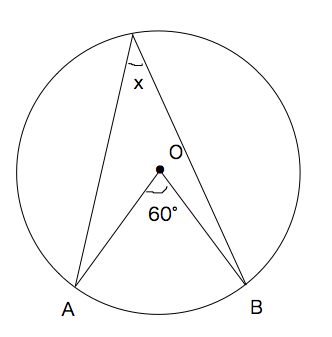
円周角の定理の基本 名前 次の()にあてはまる言葉を書きなさい。 ①1つの弧に対する円周角の大きさは( )。円周角は、 その弧に対する( )の半分である。 下の図で角xの大きさを求めなさい。 ① ② x °問題 右の図のように,円o の円周上に3 点a,b,c をとる。 ∠bac=40°のとき,∠ x の大きさを求めよ。 (北海道)(*) 解答欄 解答80°この問題では,(弧bc の円周角∠bac)= 2 1 (弧bc の中心角∠boc) よって,∠ x =70°÷2=35°



高校入試 英語 数学 円 重要問題



1
円周角と大量の二等辺1(19年度大阪府C) スポンサーリンク 短い証明の中に,大量の要素が詰め込まれていて,かなり芸術的,美しい問題です。 後で芸術的カテゴリにも追加しておこう。 大阪府の問題は,(えげつないのも多いですが)丁度X O x O 56°この問題はそれを意識してみました。 特に北海道では「は? 」という証明が出されることが他県に比べて多いので,満点取りたいなら慣れておきましょう。 円周角証明の究極系 目標時間:6分 難易度:★★★★☆ 範囲:中3円周角 <問題> <PDF,解答




円周角 補助線を引く問題



例題対比 円周角の定理
円周角の定理は円の内側で考える問題でよく使われます。 同じ弧からピザが出ていた時は円周角の定理が使えます。 同じ弧を見つけることがポイントです。 補足メモ 同じ弧が別の場所にある問題を応用問題で作りたい。円周角の定理 は,円周角と中心角について成り立つ法則です。 円で角度を求める問題では,必ずと言っていいほど活用する定理なので,しっかり覚えましょう。 円周角の定理にまつわる重要ポイントは3つです。 順に解説していきます。 ココが大事円周角の定理 (入試問題) → 携帯版は別頁 弧(こ)・弦(げん)とは 円周の一部を「弧」という. 例 右図の赤で示した部分を 弧 AB などという.(これに対して灰色で示した線分は 弦 AB という.) ※ 1つの弦により円周全体は2つの弧に分けられる




数学 中3 56 円周角の定理 基本編 Youtube
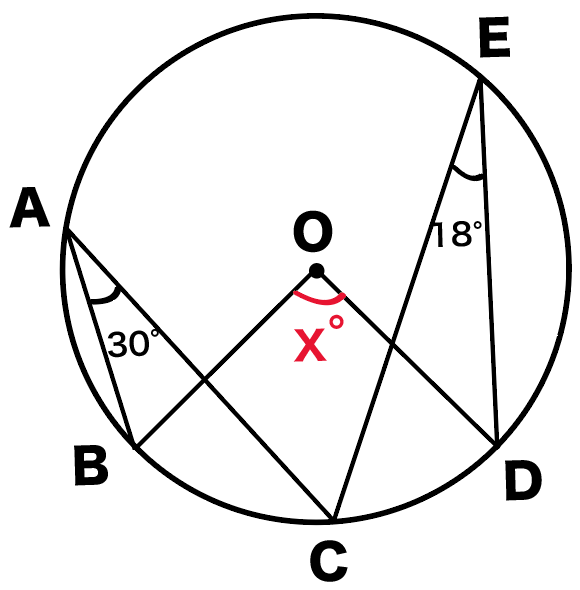



円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく
117 rows円周角と中心角(1) 問題一括 (2,462Kb) 解答一括 (2,734Kb) 円周角と中心角(2) 円周角と中心角(3) 等しい弧と円周角 円周角と図形の証明 円周角の定理の逆 円周角の定理の活用 7 三平方の定理 三平方の定理の証明(1) 問題一括 (3,793Kb) 解答一括 (4,569Kb) 三平方の
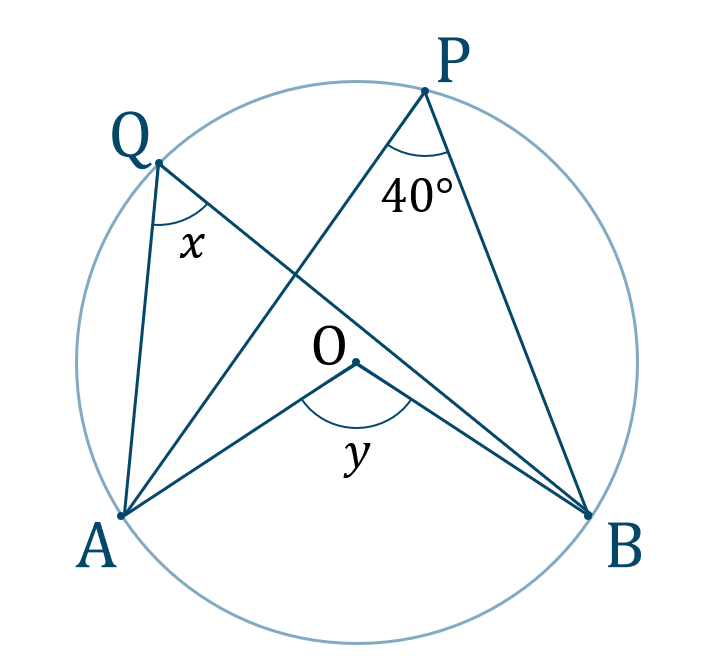



数学a 円周角と中心角の関係の使い方とコツ 教科書より詳しい高校数学



円周角と中心角 中学から数学だいすき




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




中3数学 円周角 ブーメラン型四角形 まとめと問題



円周角の定理とは 円周角の定理の証明や問題の解き方を完全解説 Studyplus スタディプラス




この問題の解き方を教えてください A B C D Eは円周を五等分する点です Clear
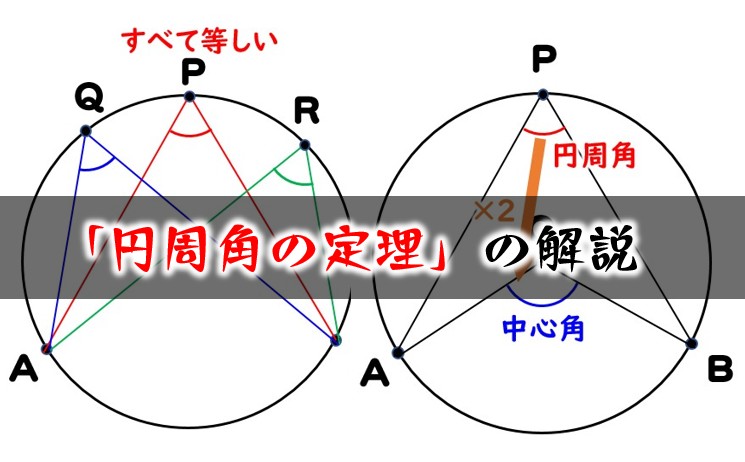



円周角の定理の解説 問題の解き方 数学fun




円の性質 円周角 図形 数学 高校受験講座 東京先生



数学の問題 解き方と答えを教えてください 円周を12等分す Yahoo 知恵袋



円周角の問題 中学から数学だいすき



円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室



円周角の定理 練習問題 苦手な数学を簡単に



1



数学円周角の定理 わかる部分だけで良いので問題の答えをお願い Yahoo 知恵袋



1




中3数学 円周角 ブーメラン型四角形 まとめと問題



中学数学 円周角の定理 例題その3 中学数学の無料オンライン学習サイトchu Su



円周角の定理 問題 Youtube



円周角の定理とは 円周角の定理の証明や問題の解き方を完全解説 Studyplus スタディプラス



中3数学 円周角の定理を使った証明の定期テスト過去問分析問題 Atstudier




円周角の定理 角度の計算方法と中心角 弧の長さの関係 リョースケ大学




中学3年の数学 動画 円周角の定理 もっと応用編の問題 19ch



中学数学 円周角 中心角




中3数学 円周角の定理を使った定期テスト予想問題 Pikuu




中学3年の数学 動画 円周角の定理 少し応用編の問題 19ch




円と角度のチェックテスト2 円周角を求める発展問題 難しい問題もあります Youtube




円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ




数学の成績を上げる方法 円周角の問題を数秒で解くコツ



数学 円周角の定理 静岡県公立高校入試問題



中学数学 円周角の定理 例題その1 中学数学の無料オンライン学習サイトchu Su




円周角 スタディーx
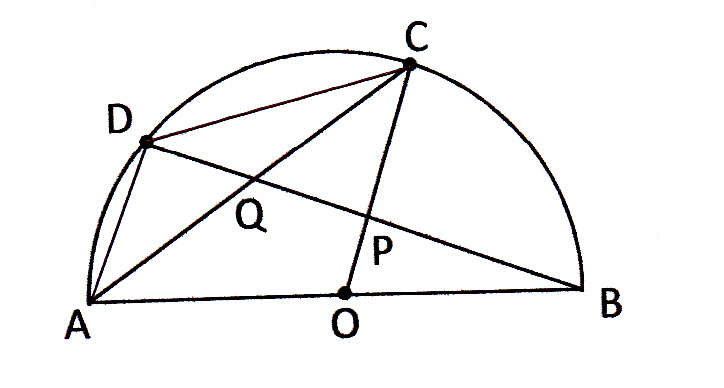



円周角の定理を使った相似の証明の解き方 現役塾講師のわかりやすい中学数学の解き方




円周角の定理の基本 計算 無料で使える中学学習プリント



円周角と比の問題 苦手な数学を簡単に
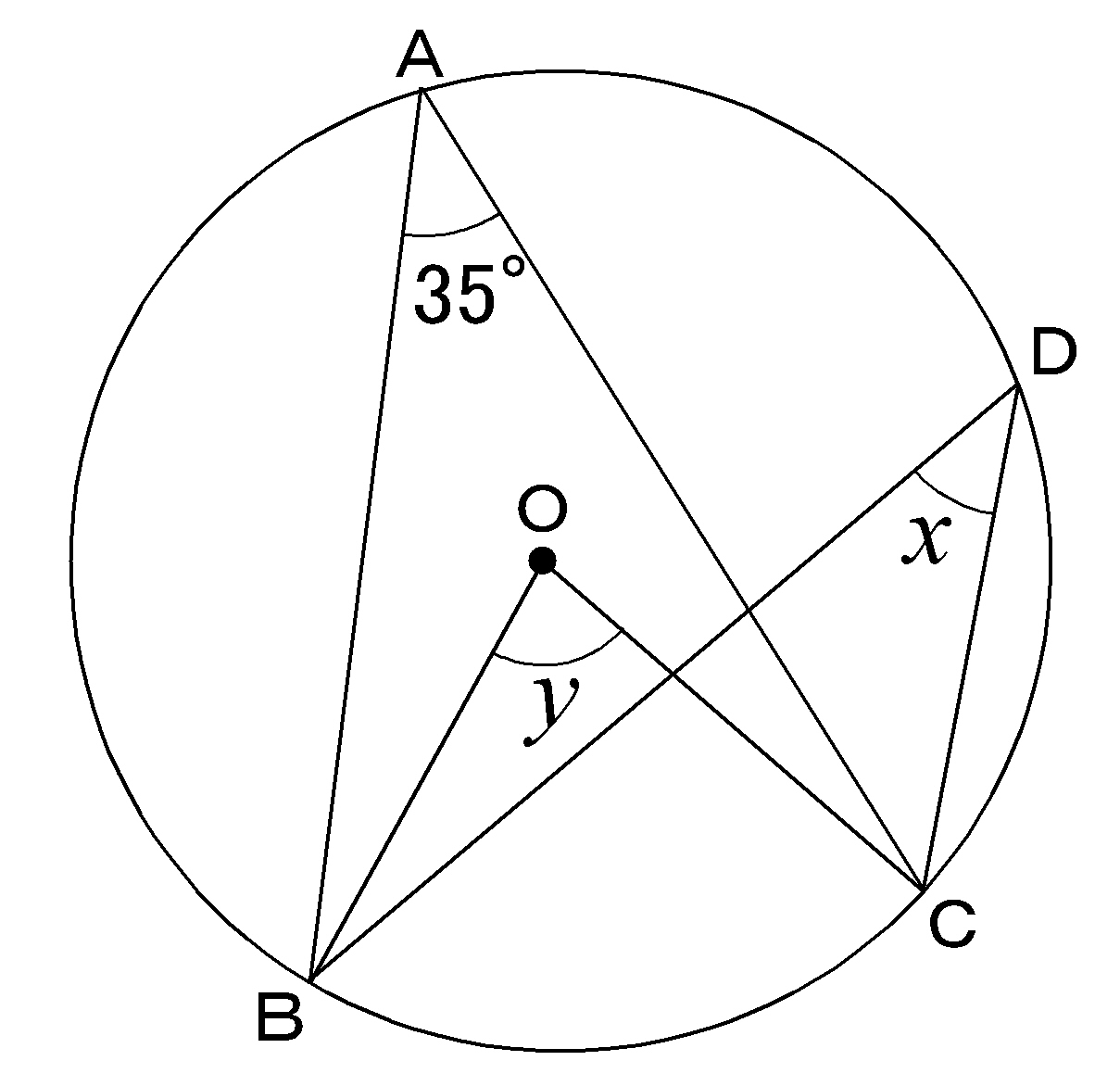



Wordで使える 円周角の問題の図 その1 Wordで数学問題プリントを作ろう
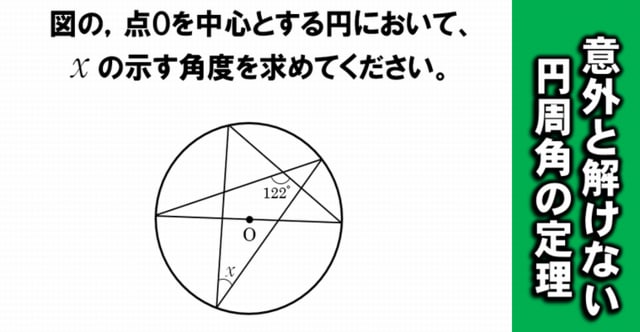



意外と解けない円周角の定理 中3レベルの数学問題 暇つぶしに動画で脳トレ




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




中3数学 円周角の定理の逆 の重要ポイント 映像授業のtry It トライイット
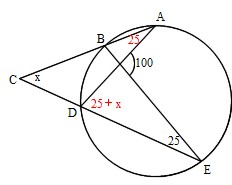



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ
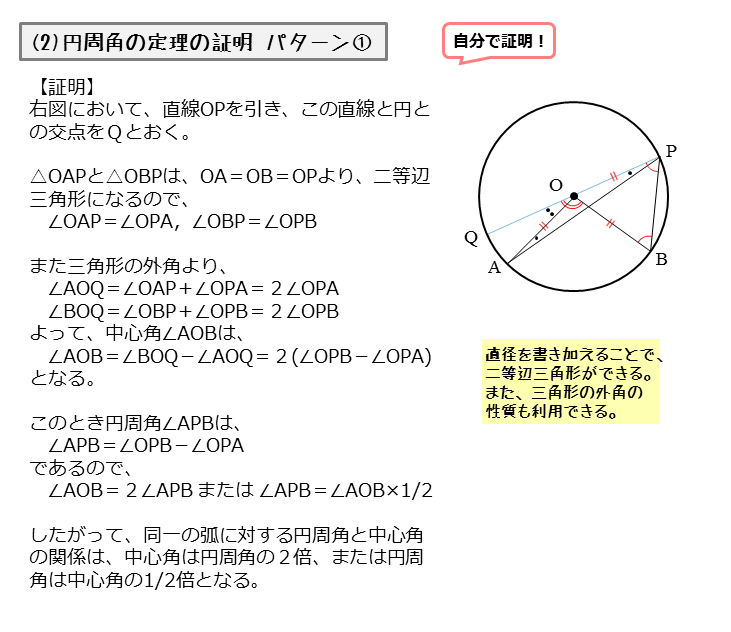



図形の性質 円周角について 日々是鍛錬 ひびこれたんれん




中学3年数学練習問題 円周角の定理の基本



三石 数学塾 2016日本数学オリンピック予選 問題3




Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ
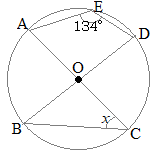



円周角の定理 入試問題




世界一わかりやすい数学問題集中3 6章 円の性質




中3数学 円周角の定理の逆 例題編 映像授業のtry It トライイット




円周角の定理の問題の解法 夢を叶える塾




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学
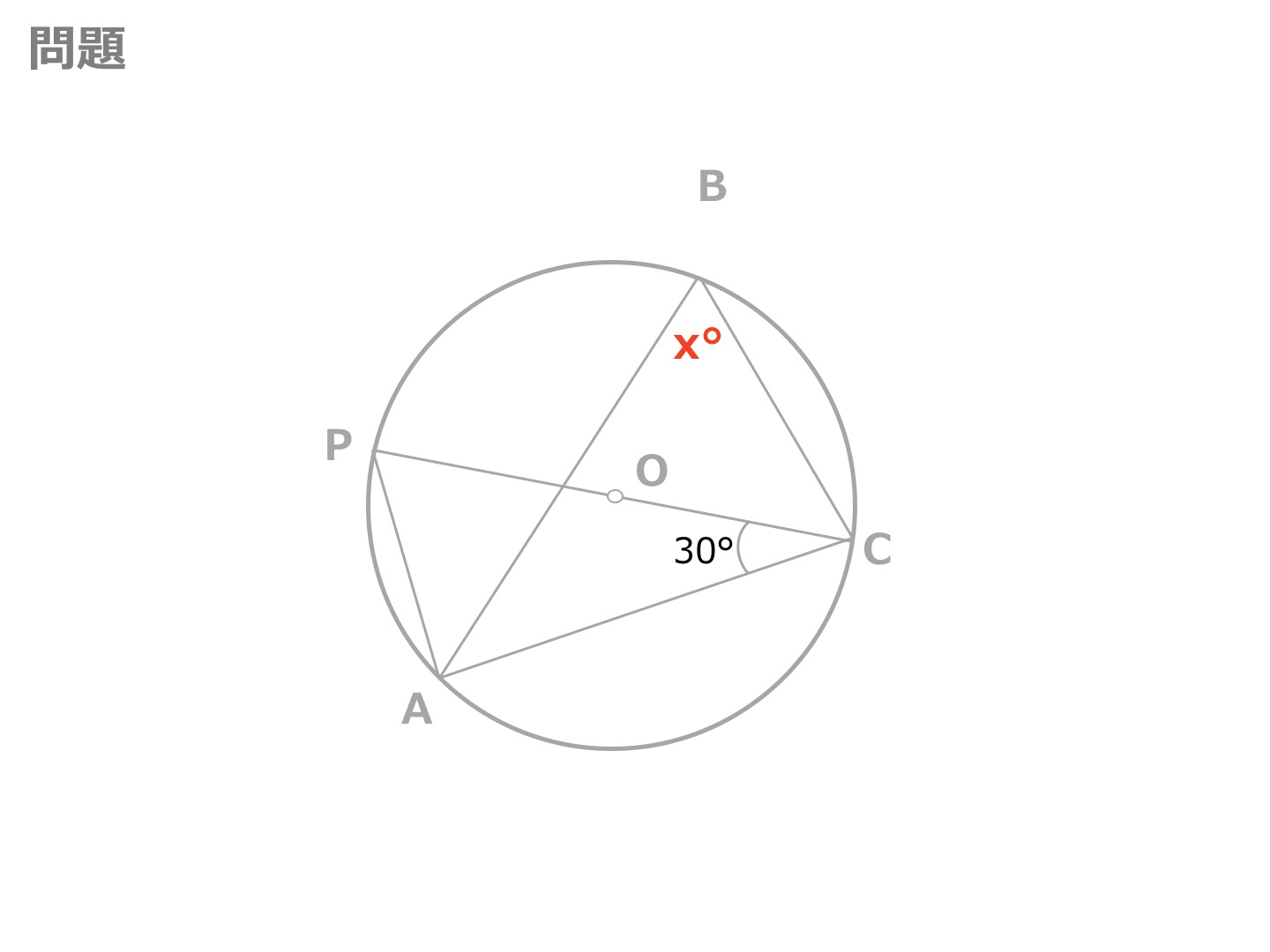



3分でわかる 円周角の定理とその逆の証明 問題の解き方 合格サプリ
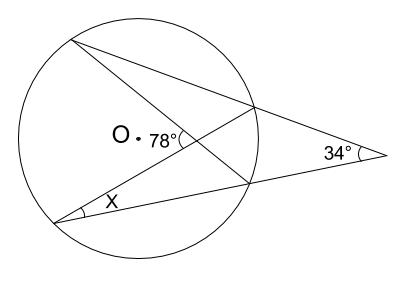



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su




中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者




円周角の定理 円に内接する四角形等図形の練習問題 中学 高校数学 身勝手な主張




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ
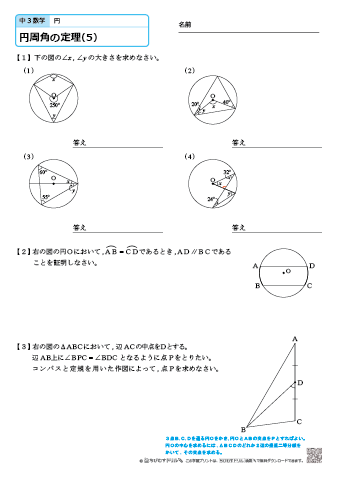



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生




円周角の定理 よくある問題 Geogebra
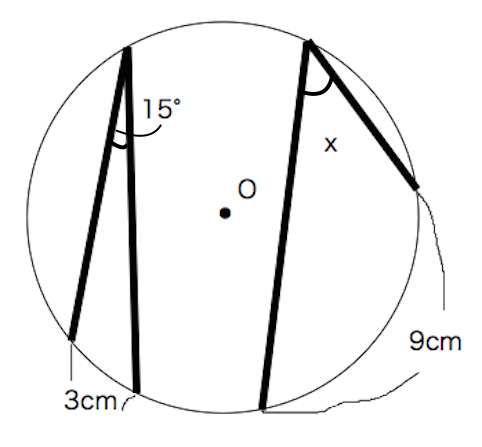



円周角の定理 練習問題 苦手な数学を簡単に




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者
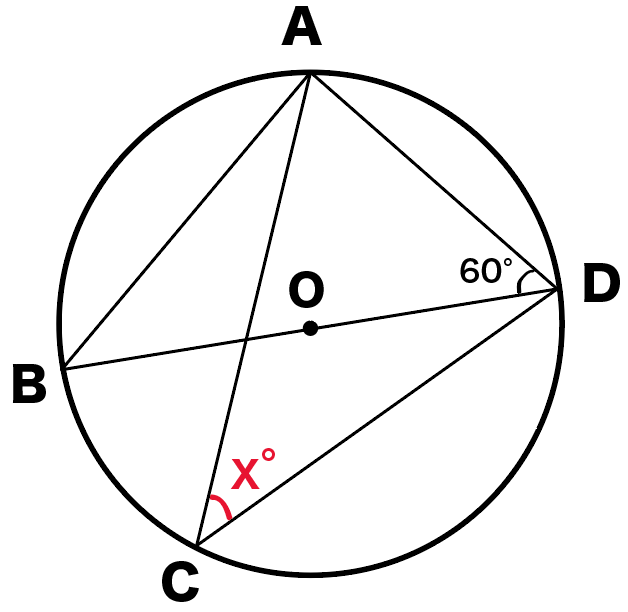



円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく
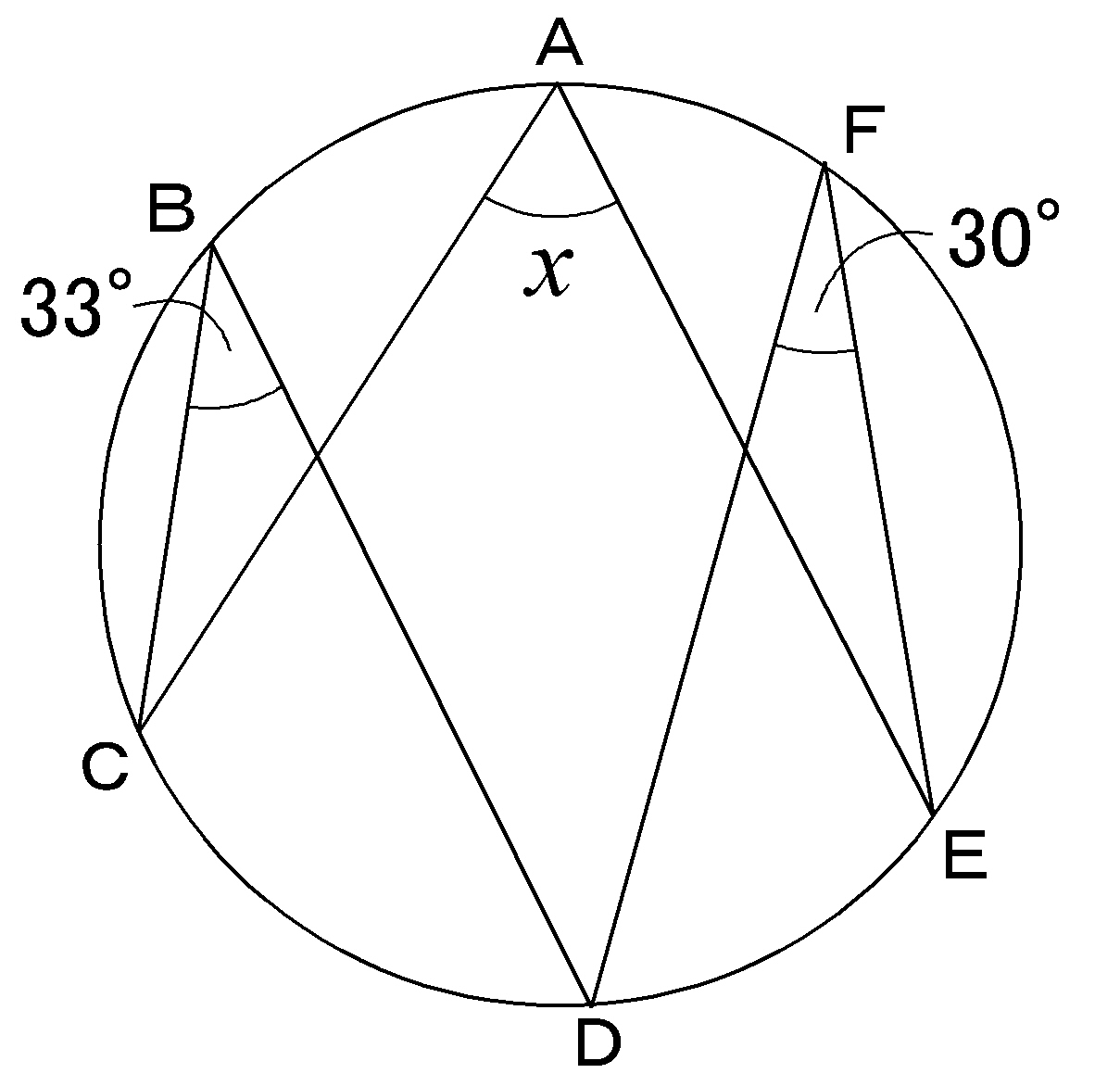



Wordで使える 円周角の問題の図 その2 Wordで数学問題プリントを作ろう
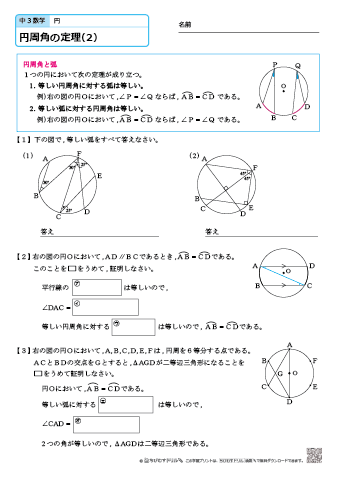



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生




円周角の定理と証明 中心角の求め方を詳しく解説 Rikeinvest
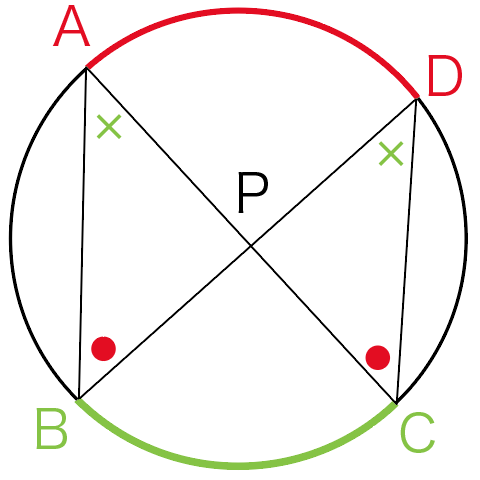



円周角の定理をつかった証明問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく



円周角の定理とは 定理の逆や証明 問題の解き方 受験辞典
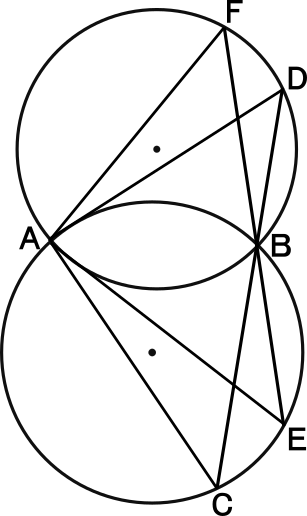



中学3年数学練習問題 円周角の定理の活用 証明問題



Tossランド 円周角の定理 の基礎 基本
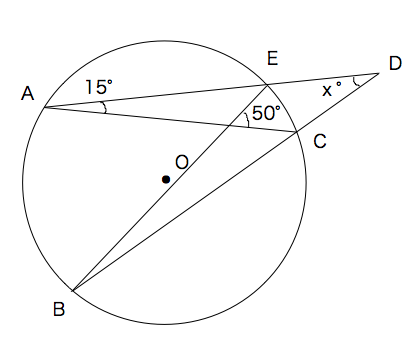



円周角の定理 練習問題 苦手な数学を簡単に



数学 円周角の定理 岩手県公立高校入試問題



中3数学 円周角の角度を求めるポイントと練習問題 中学生勉強サイトあかね先生
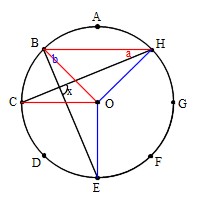



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ




世界一わかりやすい数学問題集中3 6章 円の性質




円周角の定理はこれで完璧 定理の証明と様々な問題の解法




高校数学 数a 勉強動画 円周角の定理 の問題 19ch




この2つの問題の角xの部分の解き方と答えを教えてください Clear



Math 円 4 円周角の難しい問題を解くコツ 働きアリ The 2nd




円周角の定理の逆 無料で使える中学学習プリント



円周角の定理と中心角 中学3年数学 Youtube




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者
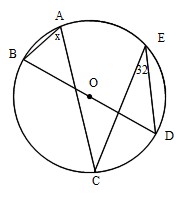



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ



ファイル 中心角と円周角 Png Wikipedia
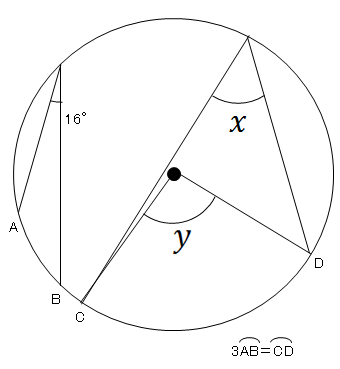



円周角 練習問題 3 ネット塾
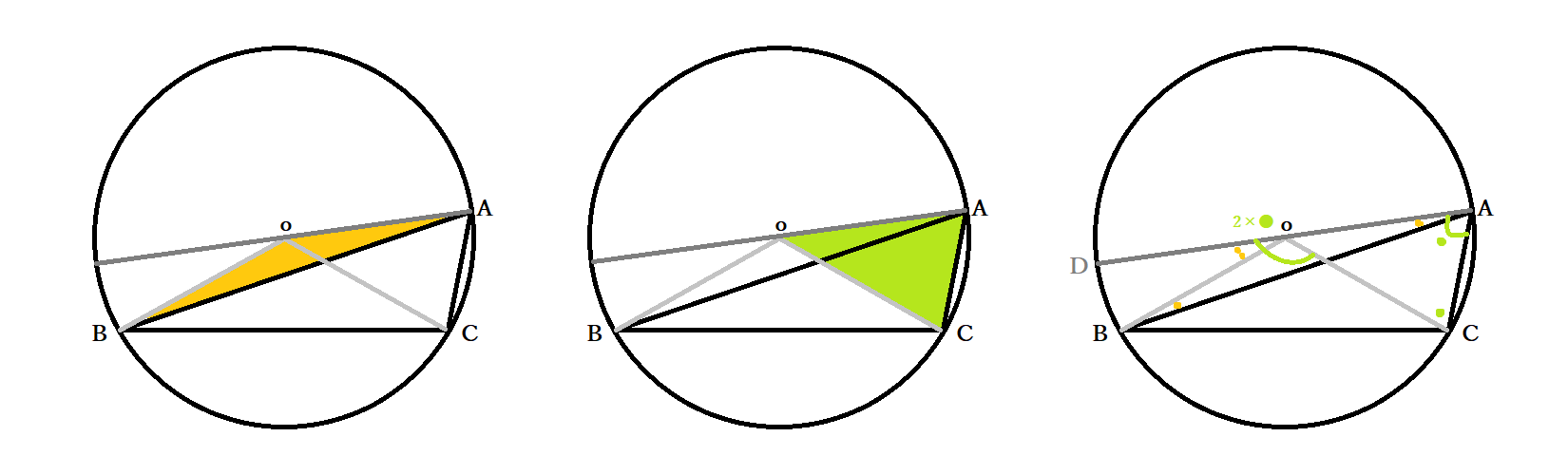



中3数学 円周角の定理とは 円周角と中心角の関係の証明法 円の性質の応用問題 中学 Curlpingの幸せblog
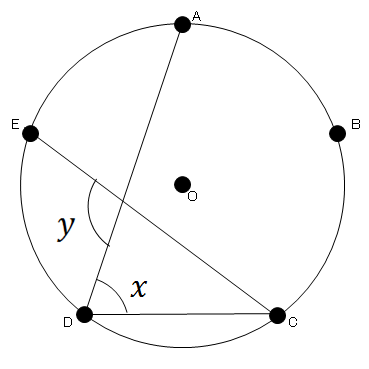



円周角 練習問題 5 ネット塾




Xの角度の求め方を教えてください 3 と 5 です 円周角の問題です Clear



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ



図形の性質 円周角について 日々是鍛錬 ひびこれたんれん



0 件のコメント:
コメントを投稿