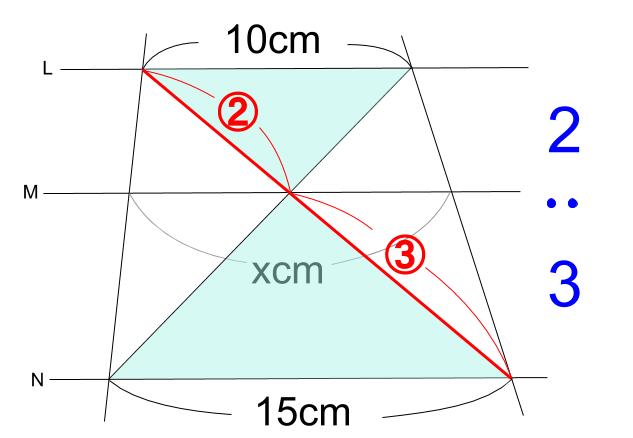
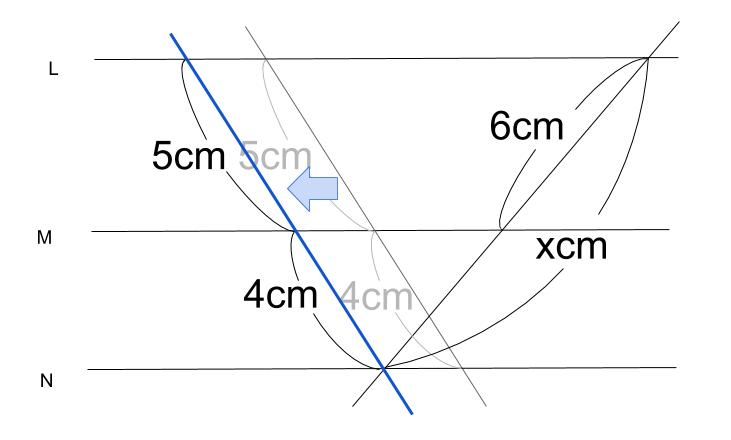
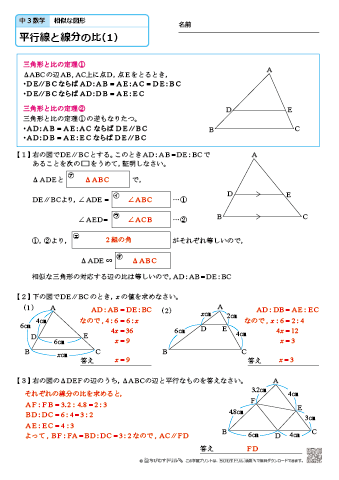
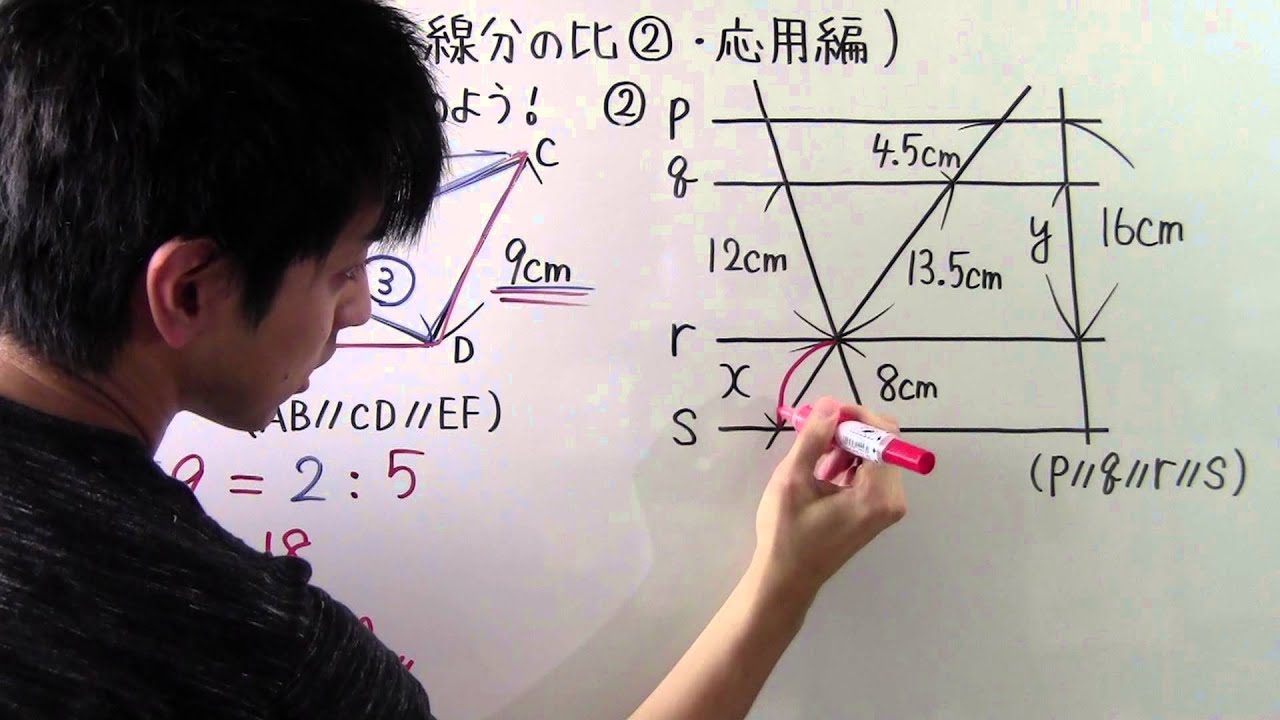
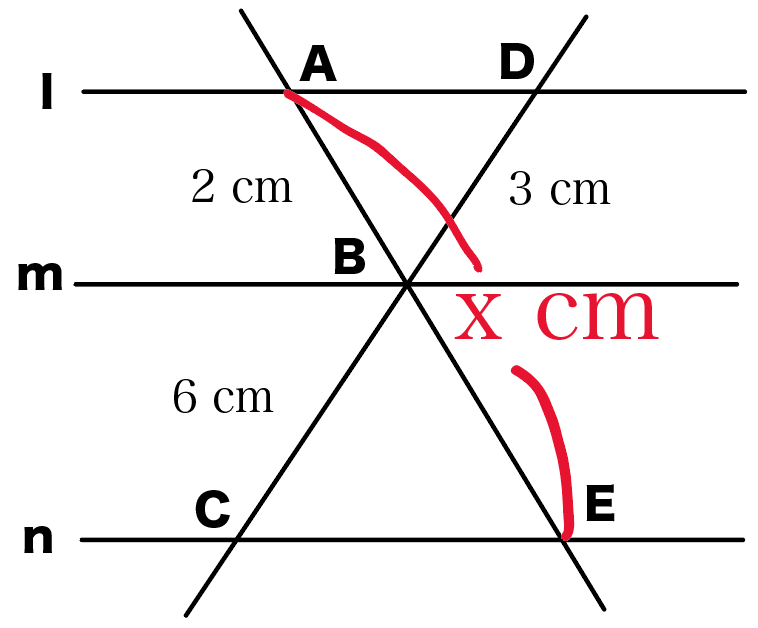
10 平行線と比の 性質を理解・ 利用する。 平行線と比の定理を理解・利用しよう。 〇平行線に直線が交わるときの線分の長さの求め 方を考え,説明する。 〇平行線と比の定理を確認する。 平行線と比の解説 平行線と線分の比の性質を覚えているかどうか、 それだけの問題ですよ。 L~M L ~ M 間と M ~N M ~ N 間との線分の比が 8 4 = 2 1 8 4 = 2 1 になる。 これを利用すれば x = 18× 2 21 = 12 x = 18 × 2 2 1 = 12 より、①平行線と角 それでは、平行線と角の特徴(性質)を見ていきましょう 人は、「特徴」があると「名前」をつけたくなりますね! 口には出さなくても、心の中で「あの『茶髪君』いけてる!」などなど、 名前をつけた、=『特徴がある』 ということですね

平行線と線分の比の定理 の問題の解き方 数学fun
平行線の性質 比
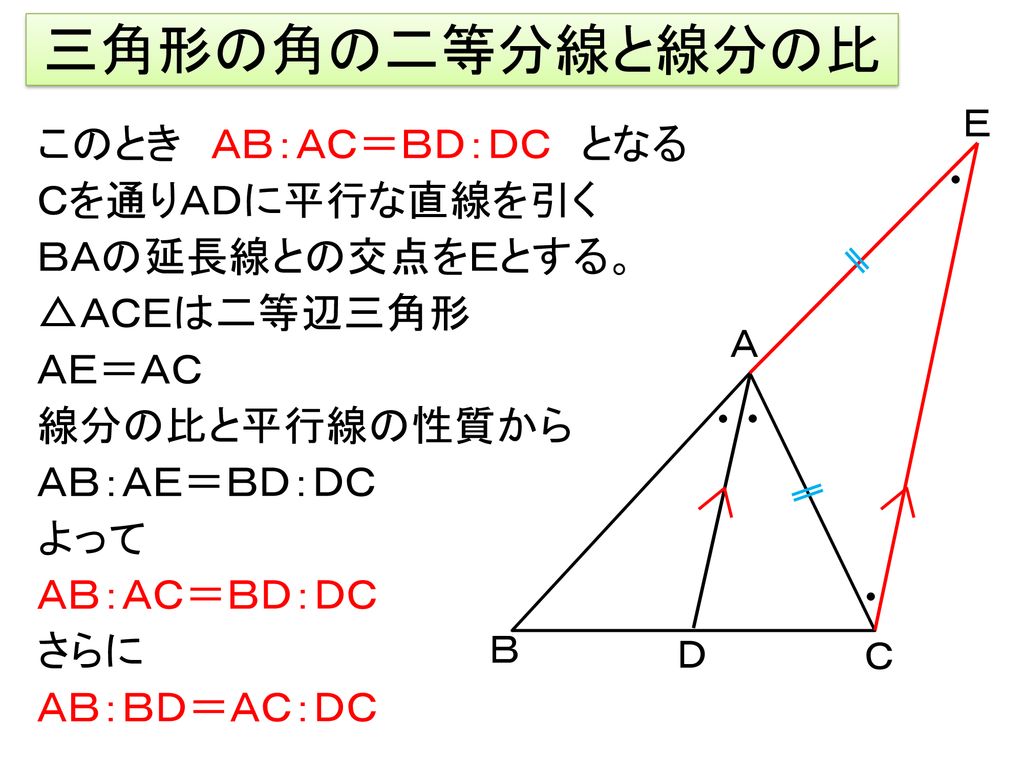
平行線の性質 比-平行線と線分の比 1 課 題 平行線の性質をもとにして、生徒たちが調べたこ とをそれぞれ生徒に説明(証明)させるという課題 学習である。生徒一人一人が自分で課題を設定し、 自分の力で証明していくのであるから、学習内容は 生徒によって異なる。 辺の比の関係式は内角の二等分線とまったく同じなので、別々に暗記する必要はありません。 ただし、二等分線と向かい合う辺の交点の位置が 元の \(\triangle \mathrm{ABC}\) の外側にある ことに注意しておきましょう。 角の二等分線の性質




角の二等分線と比の定理とは 作図方法 書き方 や性質の証明を解説 外角の問題アリ 遊ぶ数学
平行線公準問題に対する取り組み期間はフェルマーの最終定理の比ではなかった ウィキペディア にある、歴史の内容が面白い。 この公準だけ他の公準と比べて感覚的に分かるものでは無かったので、他の4公準から導き出せるのではないかと00年に渡って・平行線と線分の比についての性質を,平行線の性質や三角形の相似条件を用いて証明 することができる。 ・相似な図形の相似比と面積比及び体積比を調べ,文字式を用いるなどしてそれらの関 係について考えることができる。 (思考・判断・表現)平行線と線 分の比 平行線と線 分の比に関 する性質を 見いだし,そ れを証明し, 利用するこ とができる。 三角形の1つの 辺に平行な直線 を引き、そこに できる線分の比 について長さを 調べ、それを証 明する。 平行線と線分の 比についての性質 に関心
Mathaquarium例題図形の性質 2 平行線と比 abcの辺ab,ac上,またはそれらの延長上に それぞれ点p,qがあるとき 1 pq//bcならば ap:ab=aq:ac=pq:bc ap:pb=aq:qc 2 ap:ab=aq:acならば pq//bc ap:pb=aq:qcならば pq//bc 中点連結定理№・ 平行線と線分の比 ①本時のねらい 平行線と線分の比の性質を証明するには,三角形と比の定理を用いればよいことに気付 き,証明をすると共に,その性質を用いて線分の長さを求めることができる。 ②コンピュータ活用の意図9 2平行線 と比 ①三角形 と比 三角形における平行線と 比の性質について理解し,そ れを利用して線分の長さを 求めたり,図形の性質を証明 したりすることができる。 ノートの罫線を3等 分する方法とその方法 で3等分できるわけを 考える。
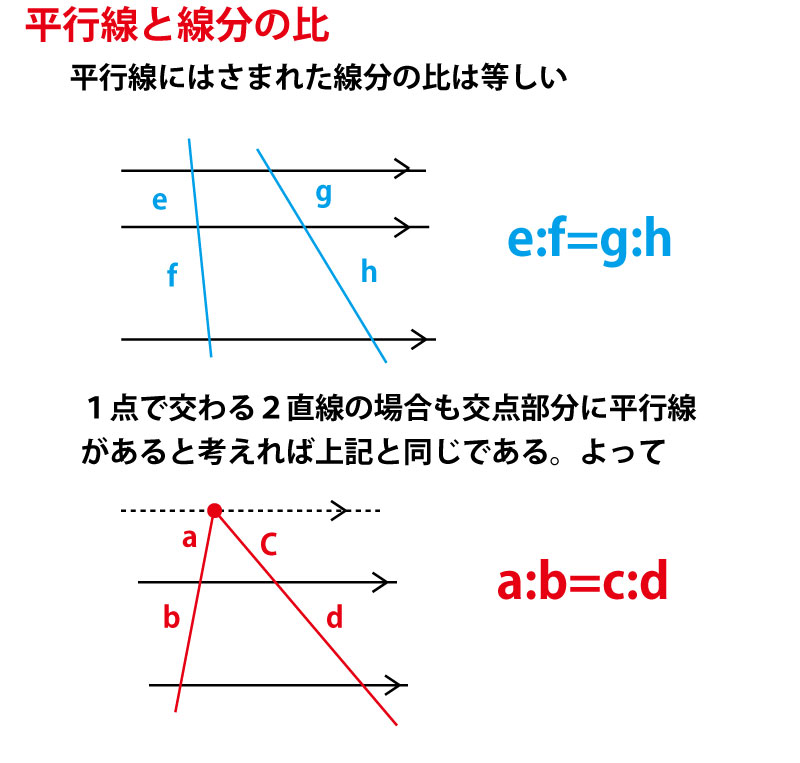
この時、点oから対応する点までの距離の比が2つの図形の相似比になる。 右の図の場合、相似比は12である。 平行線と相似 平行線と比 次に、上で得た相似の考えを用いて、一定の比を持つ平行線と交わる線分の間の 比について述べる。この映像授業では「高校 数学A 図形4 平行線の性質2」が約10分で学べます。問題を解くポイントは「2つの三角形で底辺が平行なとき、上の辺・ 図形の基本的な性質 平行線と線分の比 相似な図形の相似比と面 相似な図形の性質の活用 ※本単元「三平方の定理」 ・三平方の定理とその証明 ・三平方の定理の活用 c 図形 (5年) ・多角形、図形の合 、図形の性質 ・角柱、円柱



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学



平行線の線分比の問題の解法 夢を叶える塾
②平行線と線分の比につい ての性質を用いて,線分の 長さなどを求めることがで きる。 ③三角形と比についての性 質を用いて,線分の長さを 求めることができる。 ④中点連結定理を利用する ことができる。 ①三角形の相 似条件の意味 を理解してい る。平行線 と 線分 の 比 の 性質 を , 平行 線 の 性質 や 三角形 の 相似 を 基 に 考 察 し , 証明 することができる 。 平行線と線分の比の性質を 用いて,線分の長さや比を求 めることができる。 平行線と線分の比の 性質を理解すること ができる。 ゆうき先生 3分でわかる!平行線と線分の比の2つの証明 平行線と線分の比を証明しなきゃいけない?? ある日、数学が苦手なかなちゃんは、



本時のねらい 三角形の1辺に平行な直線が他の2辺と交わるとき それぞれの交点は その2辺を等しい比に分けることを理解する Ppt Download



中3数学 平行線と線分比の利用のポイントと練習問題
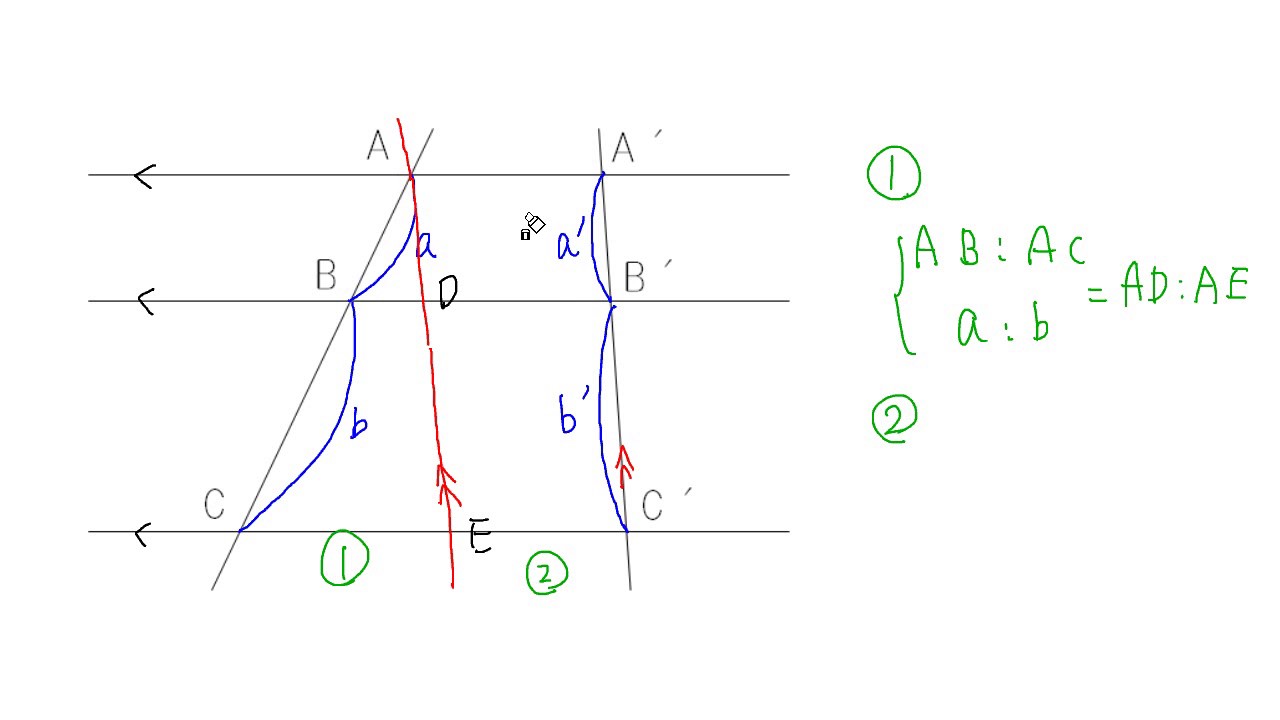
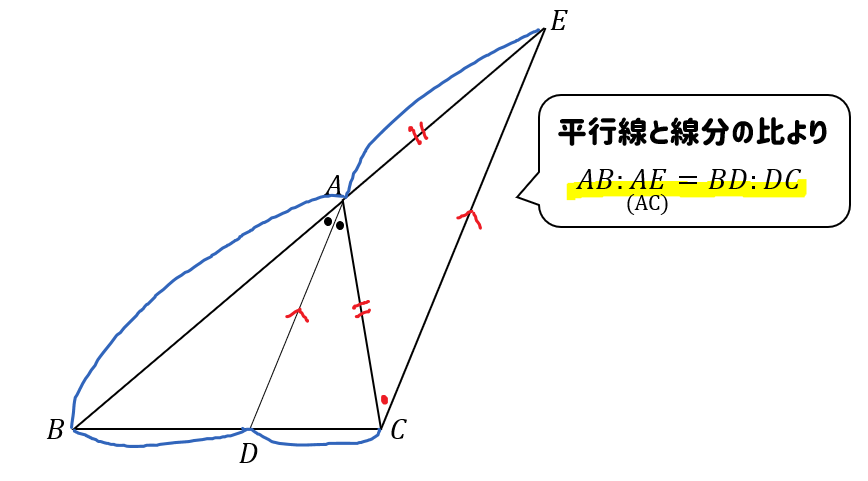
最後に、平行線と線分の比から $$\begin{eqnarray}ABAE(AC)=BDDC \end{eqnarray}$$ となります。 まとめ! お疲れ様でした! 内角の二等分線と比の性質は入試でもよく出題されます。 なので、絶対に覚えておきたいですね。平行線と線分の比 1 三角形と比(2 時間) D 本時1/2 〈目標〉 相似な図形に着目しながら,三角形と比についての性質を 理解し,比の性質 を使って長さ求め ることができ。 問題 E/BCのとき xの値を求めなさい。 〇相似な図形に着目し,な3/6 ステップ1 平行線と角度の関係(1分53秒) 4/6 パパッと分かる問題を解いてみよう(2分31秒) 5/6 ステップ2 平行四辺形の性質(1分57秒)



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく
平行線と線分の比についての性質を見いだし,それらを確かめること。 基本的な立体の相似の意味と,相似な図形の相似比と面積比及び体積比の関係について理解すること。 学習指導要領の内容項目B図形(1) <単元の評価規準>・平行線と線分の比の性 質について関心を持ち, 平行線の性質や相似条 件を用いて証明しよう としている。 ・三角形の相似条件を用 いて二つの三角形が相 似であるかどうかを考 えることができる。 ・平行線と線分の比を平 行線の性質や三角形のウ平行線と線分の比についての性質を見いだし,それらを確かめること。 エ基本的な立体の相似の意味と,相似な図形の相似比と面積比及び体積比の 関係について理解すること。 オ相似な図形の性質を具体的な場面で活用すること。 〔用語・記号〕 ∽
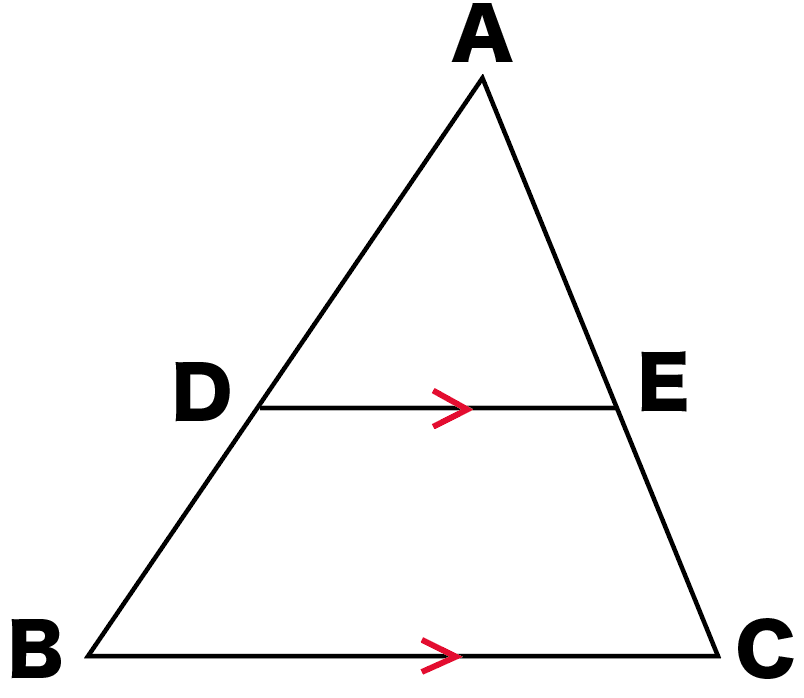



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学
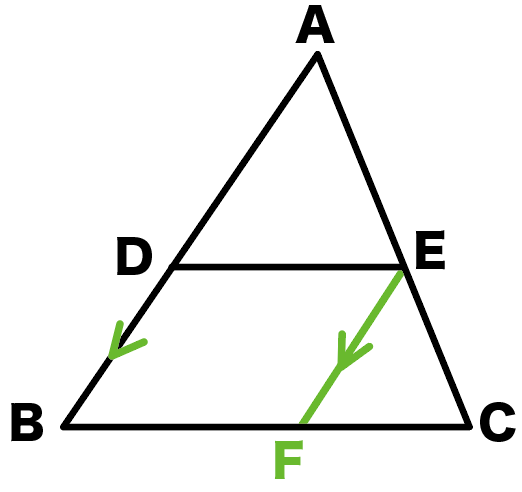
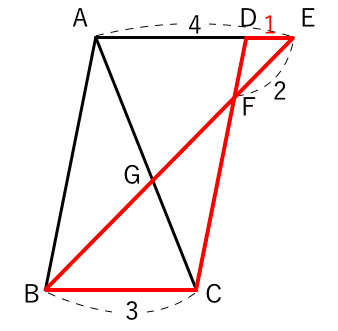
三角形と平行線の線分の比 まずは 三角形と平行線の線分の比の ルールを覚えましょう。 ポイントは ①2つの辺が平行であれば ②どの辺の比の関係が成り立つのか を押さえる というところになります。2/5時 ・ 平行線と線分の比に関する性質を理解する。 ・ 平行線と線分の比の性質を利用して、辺の長さを求めることができる。 前時のまとめを基に、平行線と線分の比の性質について確認する。 本時の学習内容「平行線と線分の比の関係について平行線と線分比 例題 練習問題 線分の内分点と外分点 例題 練習問題 線分の比と三角形の角の二等分線 例題 練習問題 面積と比 例題 練習問題 メネラウスの定理 例題 練習問題 チェバの定理 例題 練習問題 三角形の外心 例題 練習問題
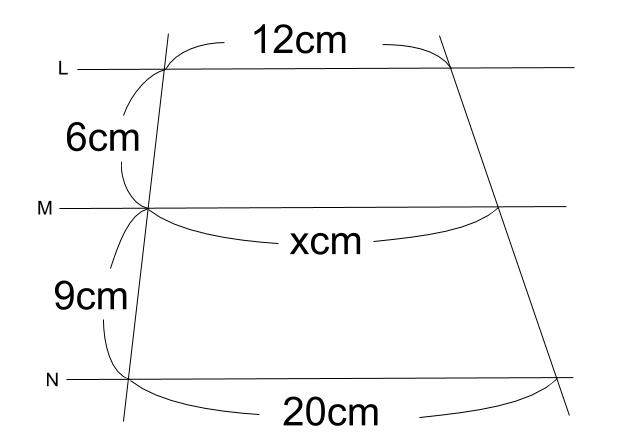



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su




平行線と比の性質の利用 Clear
12 「比と平行線」の定理の特別な場合として, ☆ 三角形の相似条件や「比と平行線」の ( 中点連結定理を考えさせる。 定理を用いて,中点連結定理を説明させ 本 る。 時 ) 課題把握,解決の見通しや平行線と線分の比につい 平行線と線分の比について 平行線と線分の比について ての性質や中点連結定理を の性質や中点連結定理を,平 の性質に関心をもち,平行線 理解し,それらを用いて, 行線の性質や三角形の相似条 の性質や三角形の相似条件を3.本時の指導(平行線と線分の比) (1) 三角形の相似に着目し,平行線と比の関係を導くことができるか。 (2) 平行線と線分の比の性質を利用し,問題解決ができるか。 (3) 複雑な問題に対して様々な考え方で対処することができるか。




数学 平行と線分比をシッカリわかると メネラウスの定理を深く理解できるよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生
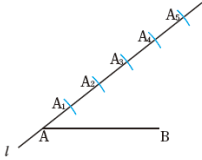



内分点と平行線の作図の仕方について 数学 苦手解決q A 進研ゼミ高校講座
比の相等関係 中学2年 「図形の性質と合同」 ・角と平行線 ・三角形の合同・証明 中学1年 「平面図形」 ・平面図形の観察 ・平面図形の作図 小学5年 平行四辺形,ひし形,台形 の定義および基本的性質 小学5年 ・平行線の定義と性質の相似条件,平行線と 線分の比についての 性質,相似比と面積比 及び体積比の関係な どを理解し,知識を身 に付けている。 4 単元について (1) 単元について 学習指導要領の第3学年の目標(2)に「図形の相似,円周角と中心角の関係や三平方の定理平行線と比の定理を用いて図形の 性質を考察し性質を考察し, ,,,線分の長さを求めた線分の長さを求めた り証明したりすることができるよ うにさせる。うにさせる。 ⑥三角形と比の定理や中点連結定理, 平行線と比の定理を図・言葉・式で
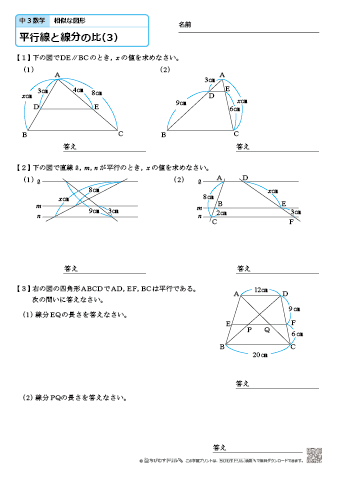



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



平行線と線分の比 Youtube
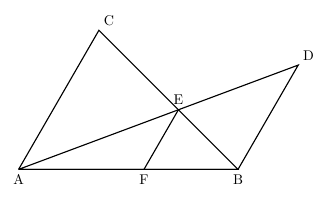
内角の二等分線と比 a b d c 4abc の˛a の内角の二等分線と辺bc との交点をd とすると 点d は線分bc をab ac に内分する すなわち ab ac = bd dc ⃝注逆も成り立つ. a b d c e ' ⃝考(平行線を考える) ⃝あ ab ‚ ac のとき 直線ad に平行で点c を通る直線を' とする.平行線と比の性質を利用して、図形の性質を考察し、証明することができる。 (3)本時の展開 6.家庭での課題(家庭との連携)と本時の関わりについて 家庭で授業の内容を振り返りながら様々な証明方法を考えることで、三角形の角の二等・ 線分の比と平行線の性質を利用して、問題を解決することができる。 段階 学習活動 数学的活動を通した指導のポイント ( は数学的活動をともなう学習活動)



中学数学 平行線と線分の比 その1 中学数学の無料オンライン学習サイトchu Su



サクッと解説 角の二等分線と比の特徴となぜ について 数スタ
イ 平行線と線分の比の性質を使って、いろいろな線分の長さを求めることができる。 (2)指導の構想 ア 本時の課題の設定や問題解決の場面、まとめの場面において、生徒の考えや言葉を利用する平行線と比(2) ・平行線と線分の比の性質を利用行動観察 2 ・平行線と比の定理 して,線分の長さを求めることが発表 ・平行線と比の定理を利用して できる。 自己評価 線分の長さを求めたり,線分 ・平行線と比の性質を理解してい を等分する る。



1




サクッと解説 角の二等分線と比の特徴となぜ について 数スタ



平行線と線分の比 辺の長さを求める応用問題4選 教遊者
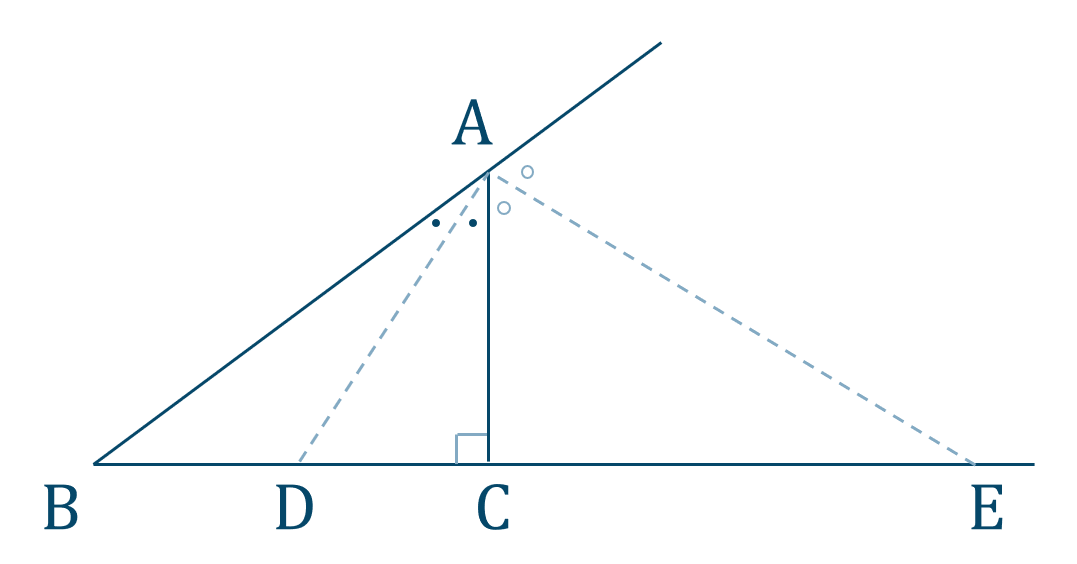



数学a 角の二等分線と比の使い方とコツ 教科書より詳しい高校数学




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




中学数学 平行線と角 平行線の性質 Youtube




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学
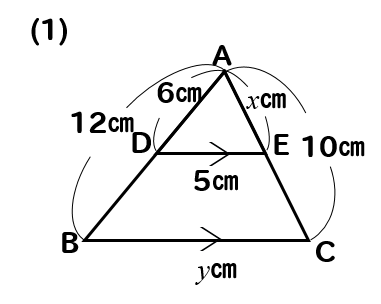



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ




高校数学a 平行線の性質のおさらい1 同位角 錯角 映像授業のtry It トライイット



平行線と線分の比 辺の長さを求める応用問題4選 教遊者




角の二等分線と比の定理とは 作図方法 書き方 や性質の証明を解説 外角の問題アリ 遊ぶ数学




角の二等分線が図で誰でも一発でわかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




平行線と線分の比 の問題のわからないを5分で解決 映像授業のtry It トライイット
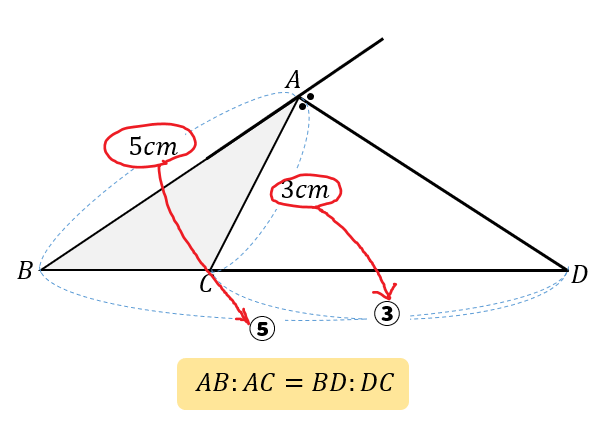



サクッと解説 角の二等分線と比の特徴となぜ について 数スタ




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典
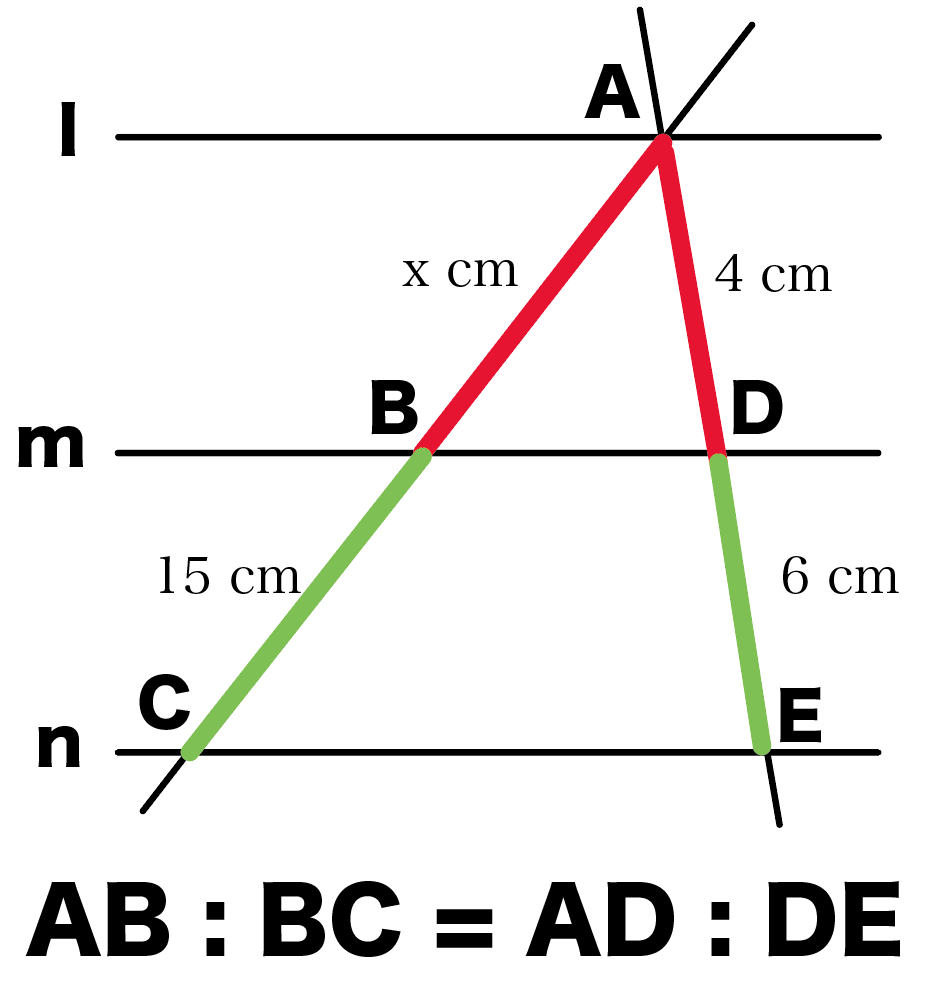



平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




平行線と線分の比 中学校数学 2018年度高崎経済大学経済学部 地域政策学部入試問題 身勝手な主張
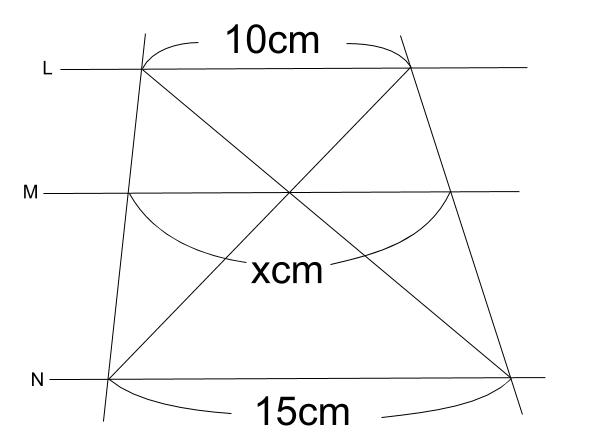



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su




相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ
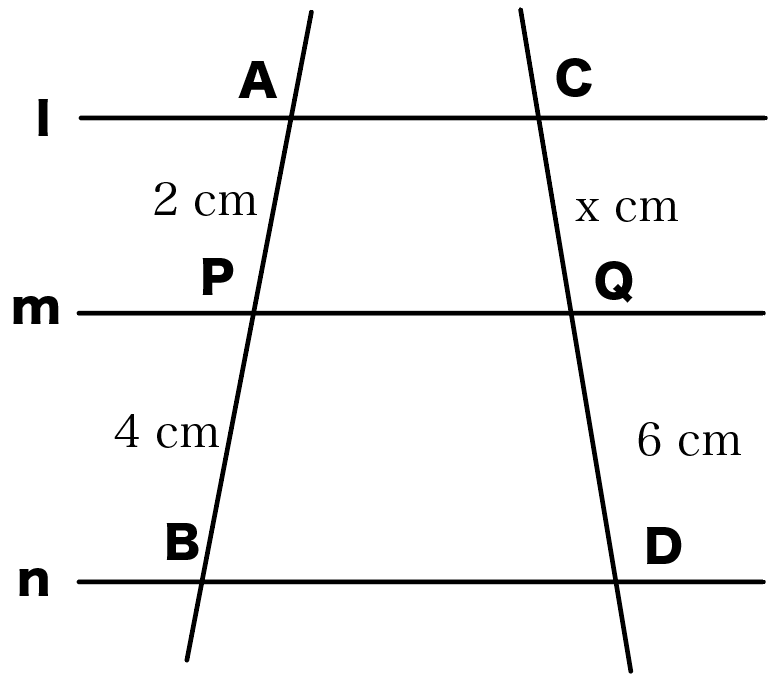



平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
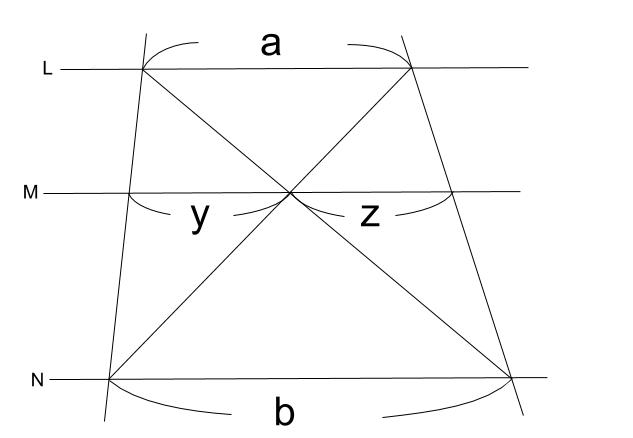



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su




平行線と線分の比の定理 の問題の解き方 数学fun




中3数学 相似 台形の対角線 Youtube




平行線と線分の比の定理 の問題の解き方 数学fun




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学
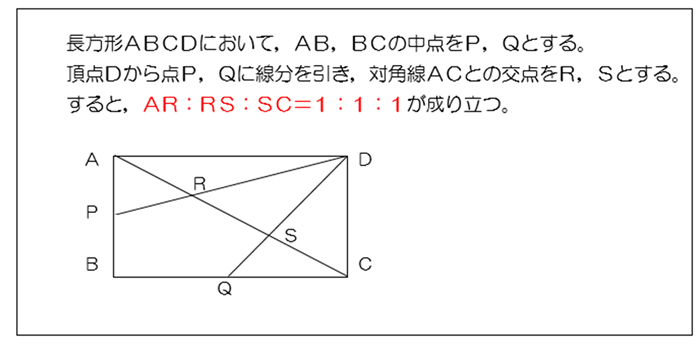



授業実践記録 数学 新しい 定理 とその活用 啓林館
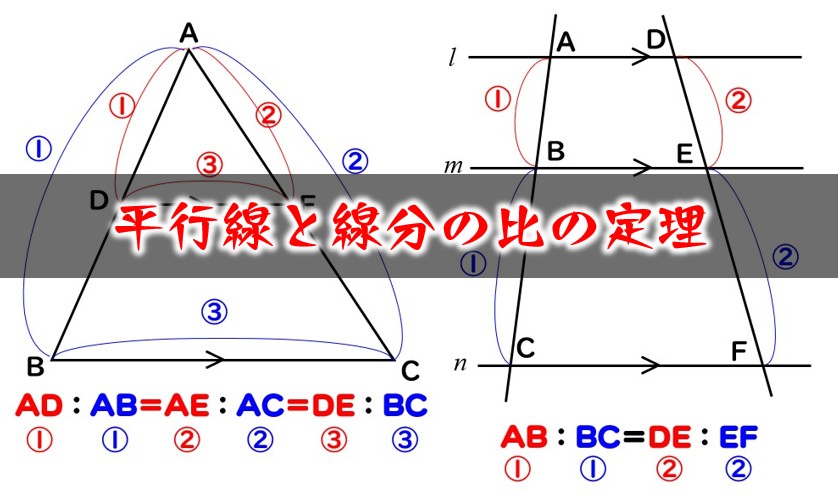



平行線と線分の比の定理 の問題の解き方 数学fun
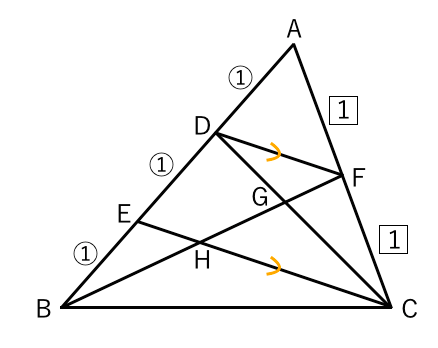



相似な図形 平行線と線分の比 よく出る系 苦手な数学を簡単に
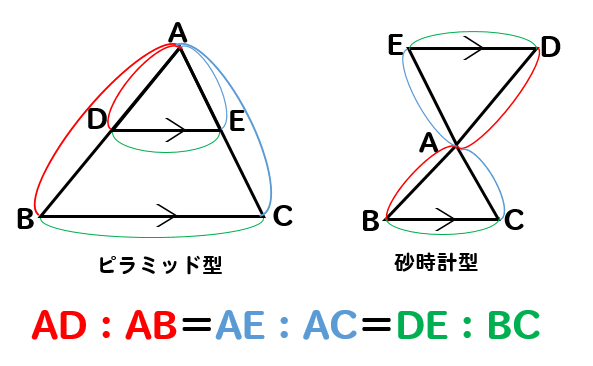



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ




中学数学3 平行線と線分の比の証明 中学数学 By となりがトトロ マナペディア



1
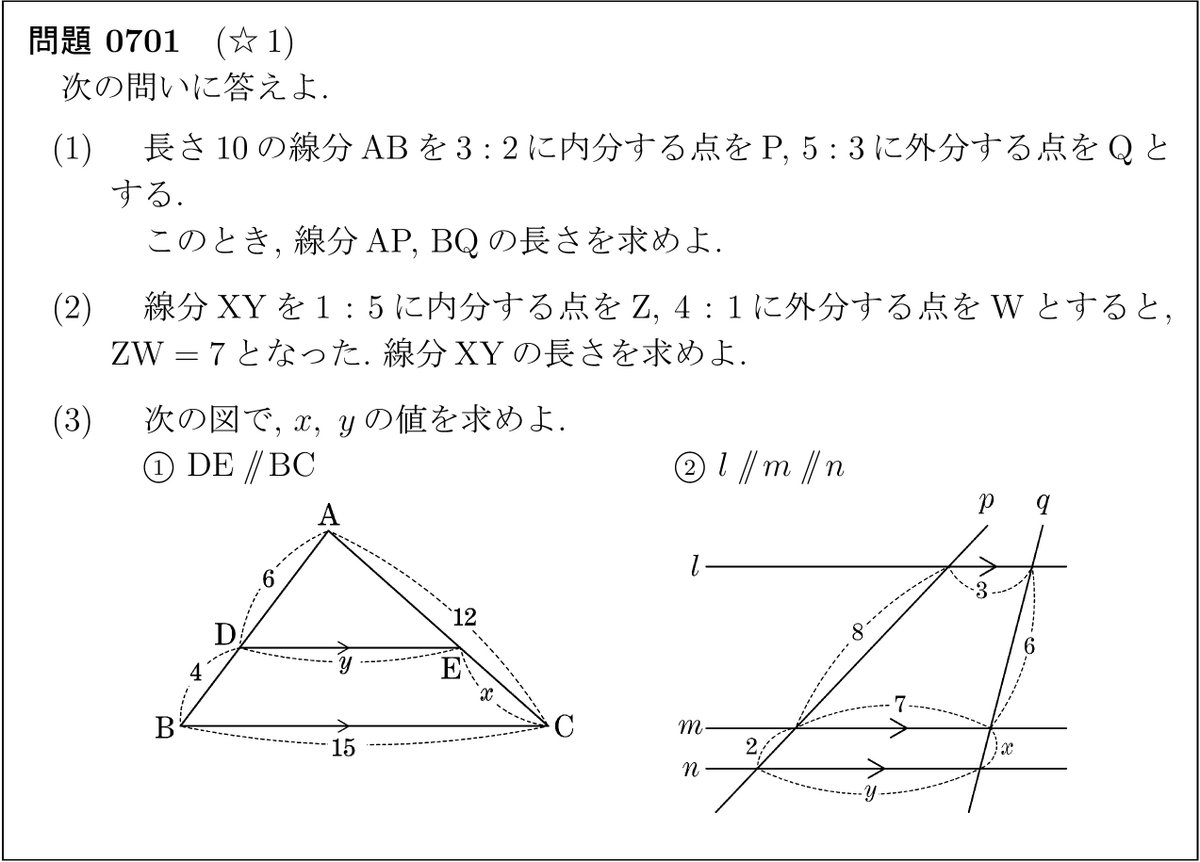



高校数学基本問題垂れ流し 07 図形の性質 1 三角形と比 線分の内分と外分 平行線と比 T Co Rvv5doaz7m



1




平行線と線分の比の定理 の問題の解き方 数学fun




平行線と線分の比 三角形の比の取り方を簡単な問題で覚えよう 中学や高校の数学の計算問題




中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




この問題って 線を引かないとできないと思うんですけど その線って角度とか長さとか Clear



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中3数学 相似の平行線と線分の比のポイントと定期テスト対策問題




平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




平行線と線分の比の定理 の問題の解き方 数学fun



数学 中3 50 平行線と線分の比 応用編 Youtube



16年前期 千葉県公立高校入試 数学 第2問 5 作図 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su




平行線と線分の比の問題 平行な3つの直線が2つの直線と交わっています 数学 教えて Goo



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に
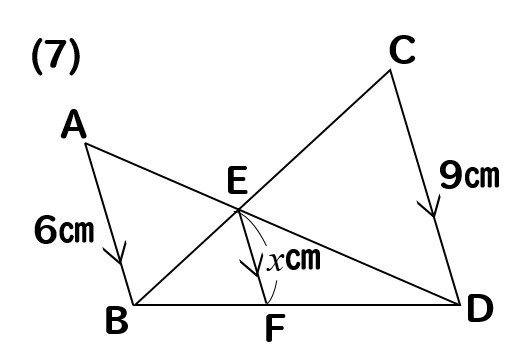



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ



Studydoctor平行線と線分の比の利用 中3数学 Studydoctor
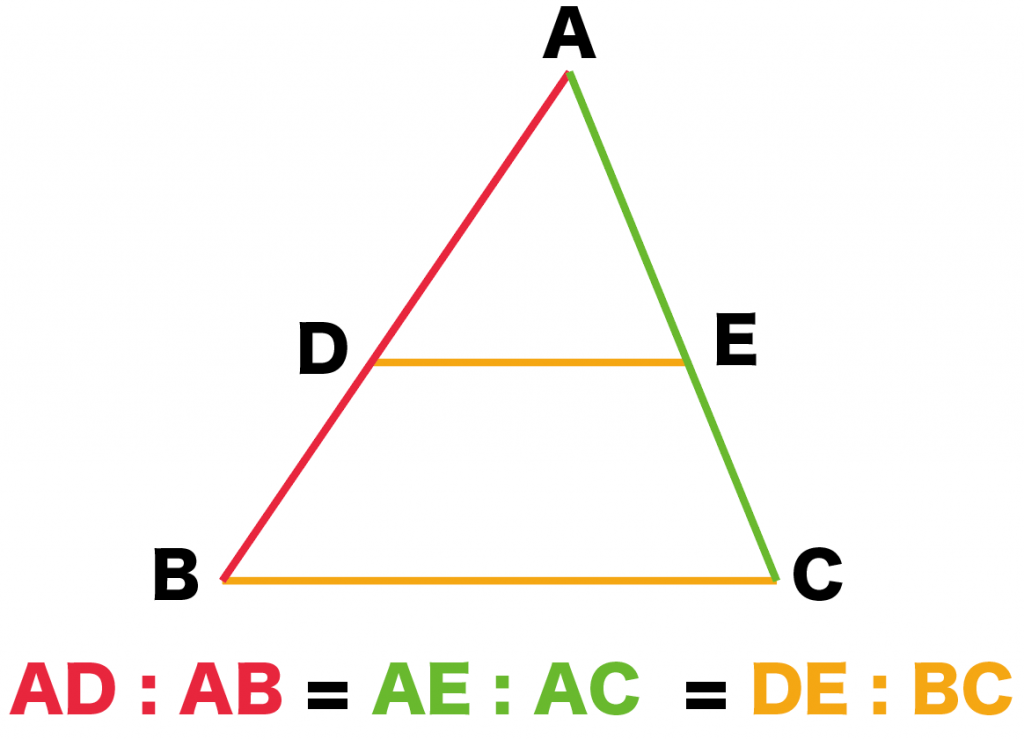



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく



相似な図形の考え方について質問です 中学三年生の学習内容 Yahoo 知恵袋




高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月



平行線の比




平行線と線分の比の定理 の問題の解き方 数学fun



Studydoctor平行線と台形 中3数学 Studydoctor
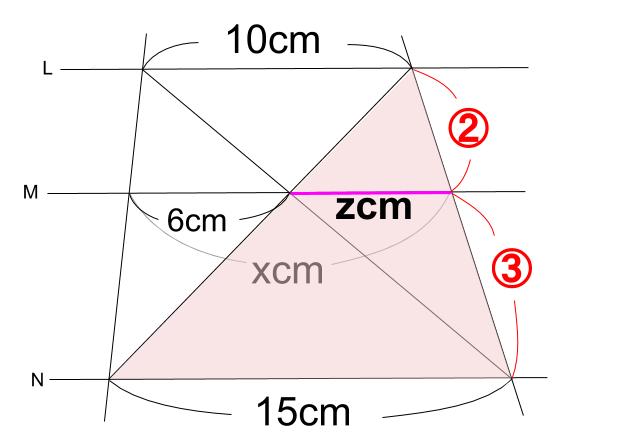



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su
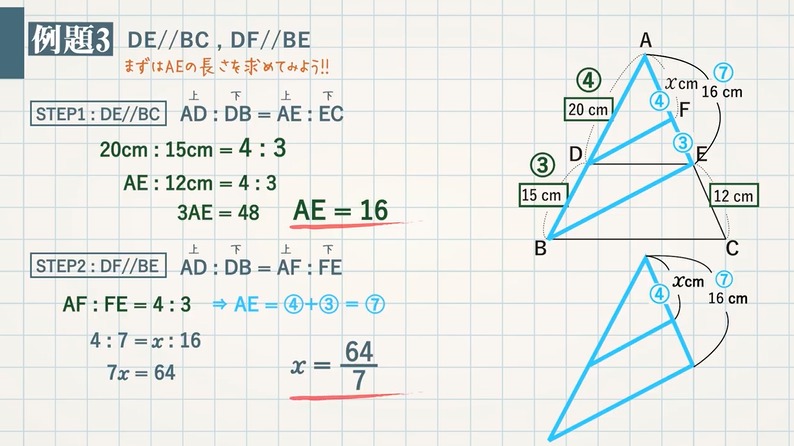



平行線と線分の比 辺の長さを求める応用問題4選 教遊者




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




高校数学a 角の二等分線と比の利用 練習編 映像授業のtry It トライイット




平行線と線分の比 中学校数学 2018年度高崎経済大学経済学部 地域政策学部入試問題 身勝手な主張



平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




数学 中3 49 平行線と線分の比 基本編 Youtube



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典
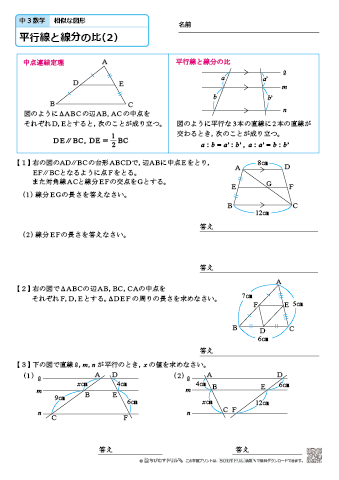



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
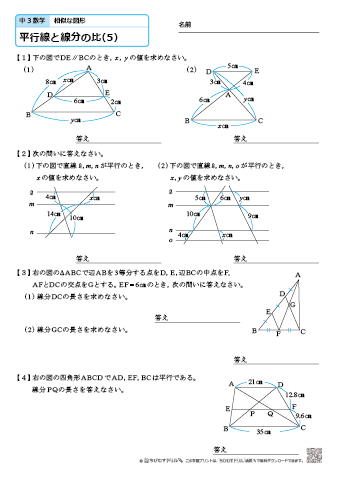



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




公式一覧と使い方 解き方 数学a 図形の性質 教科書より詳しい高校数学
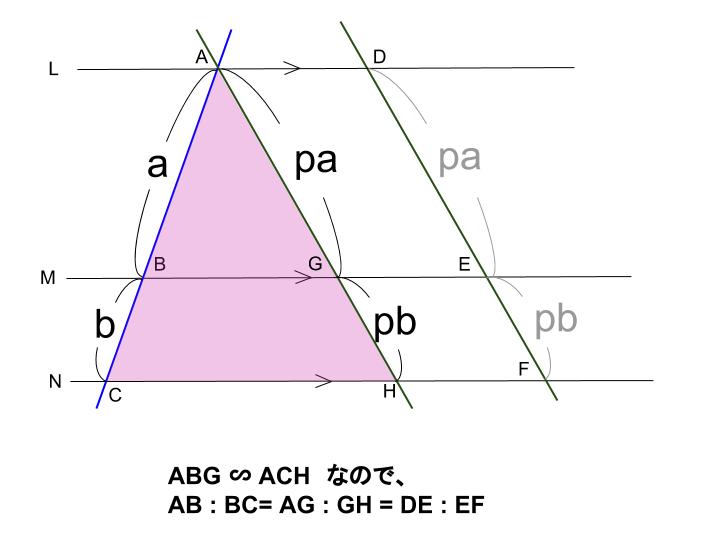



中学数学 平行線と線分の比 その1 中学数学の無料オンライン学習サイトchu Su
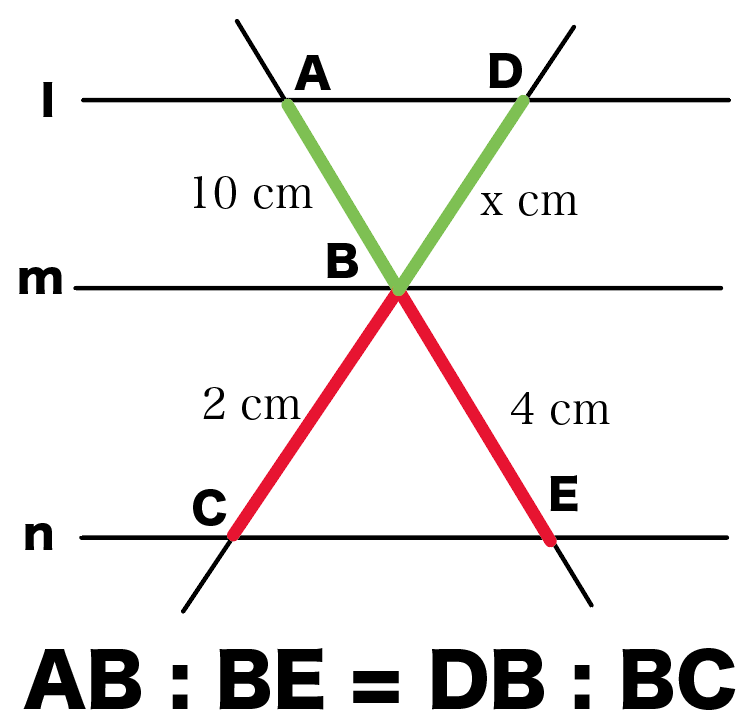



平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
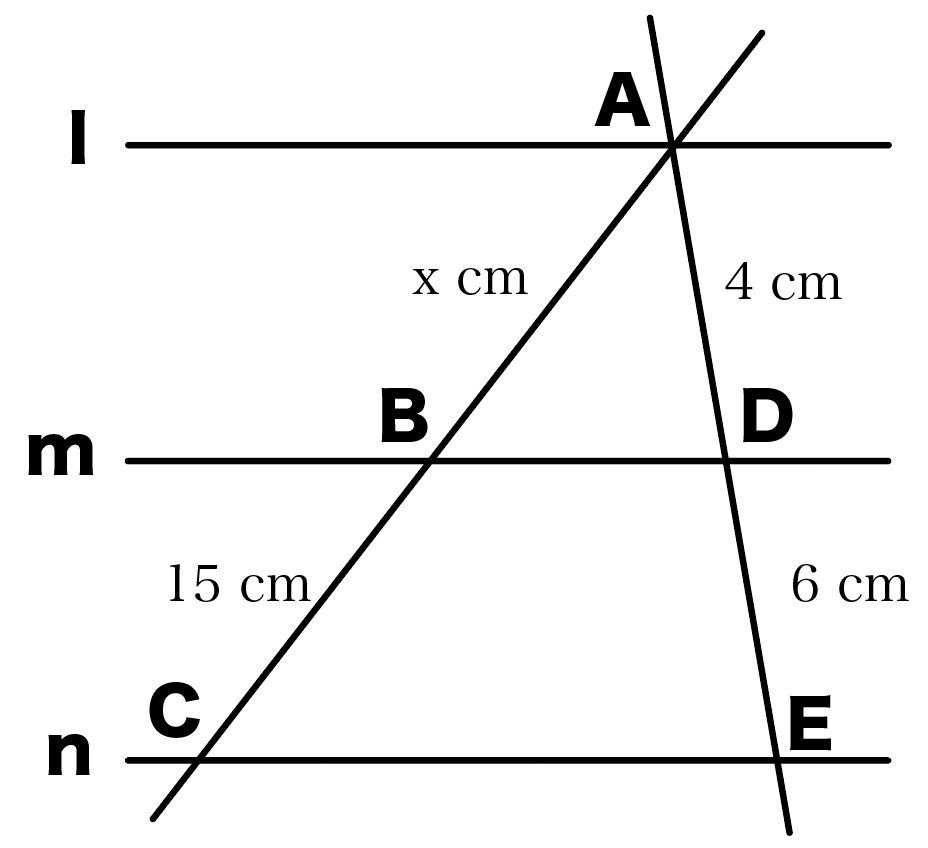



平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
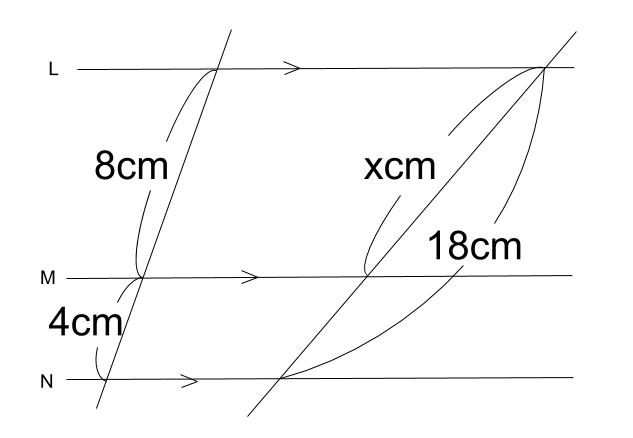



中学数学 平行線と線分の比 その1 中学数学の無料オンライン学習サイトchu Su



次の図において Xの値を求めよ という問題です 数学a平行線の性 Yahoo 知恵袋
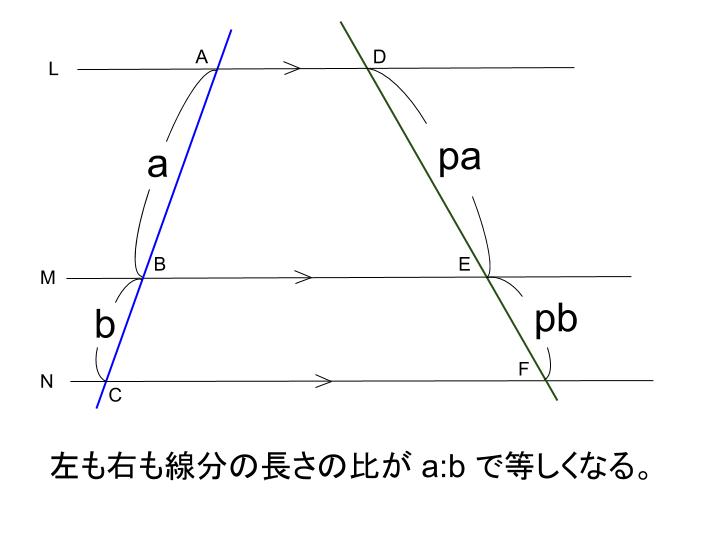



中学数学 平行線と線分の比 その1 中学数学の無料オンライン学習サイトchu Su



1



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学
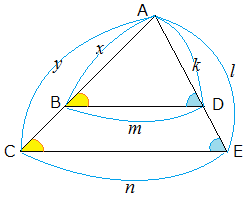



平行線と線分の比




平行線と線分の比 の問題のわからないを5分で解決 映像授業のtry It トライイット
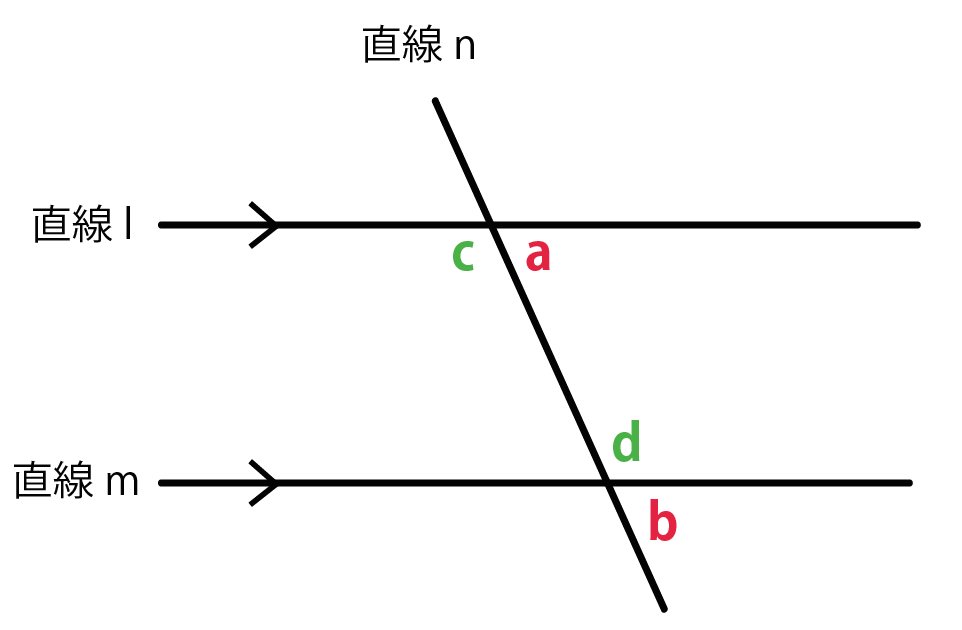



同位角 錯角 平行線の性質で問題を2秒でクリアする方法 Qikeru 学びを楽しくわかりやすく
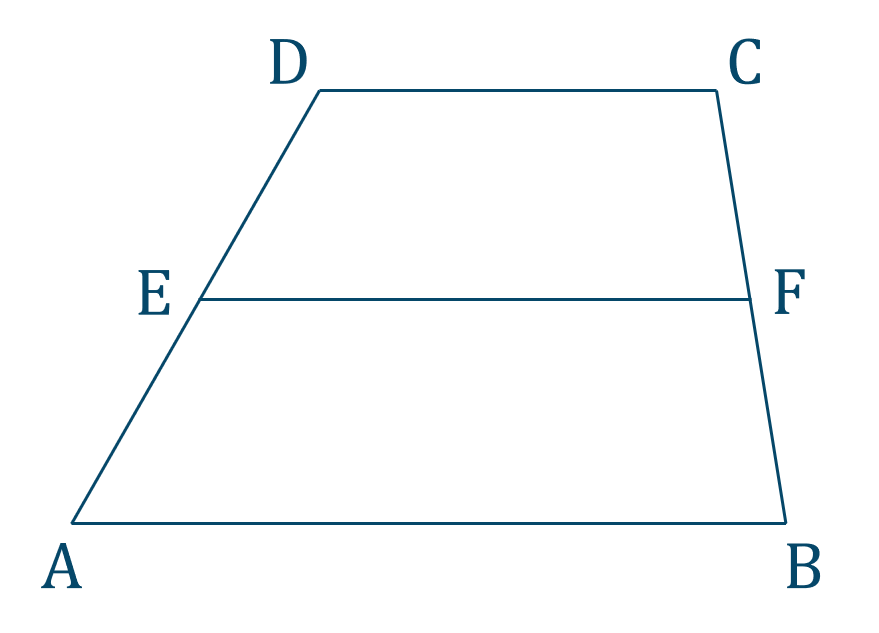



教科書レベルの問題一覧と解答 数学a 図形の性質 教科書より詳しい高校数学
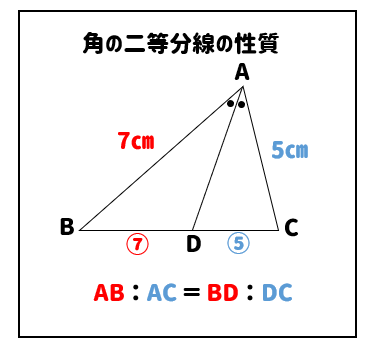



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ
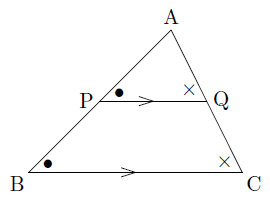



平行線と線分の比 まなびの学園




平行線と線分の比 の問題のわからないを5分で解決 映像授業のtry It トライイット
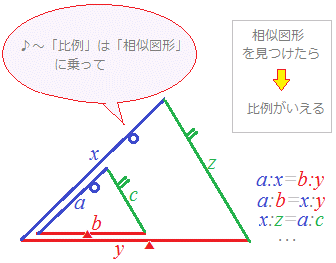



平行線と線分の比




内角の二等分線 外角の二等分線の比の定理 証明 Youtube
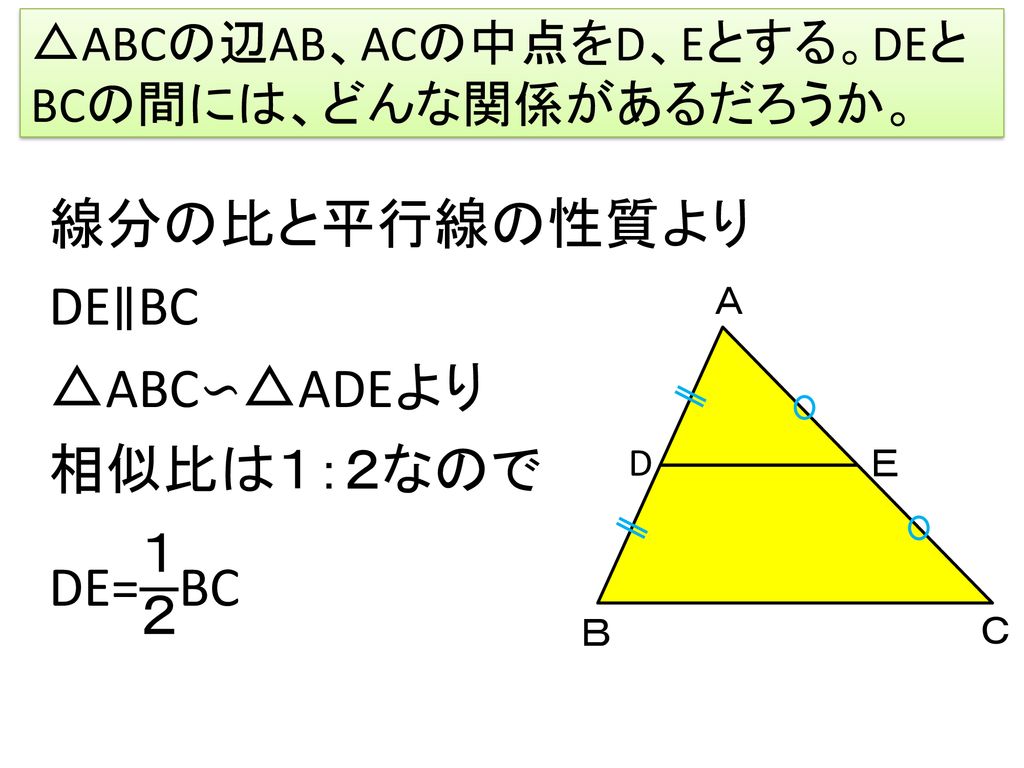



中点連結定理 本時の目標 中点連結定理を理解する Ppt Download
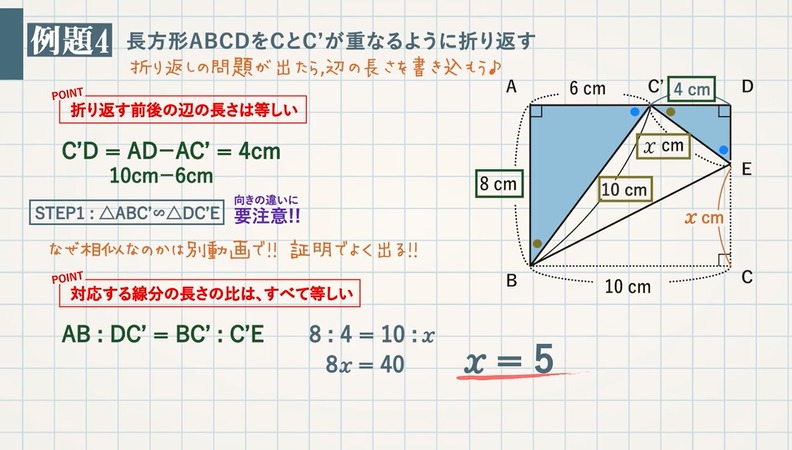



平行線と線分の比 辺の長さを求める応用問題4選 教遊者




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学



0 件のコメント:
コメントを投稿