(2)bとcは何分ごとに出会いますか。( 分) (大阪桐蔭中 08年 ユニーク入試) <問題1の考え方と答え> 旅人算の問題のパターンに、池や遊歩道のような「周」を回るものと、ある区間を往復するという2つがあります。折り返しは、出会い問題として推理する 例題1-① ①折り返し問題は、「出会い問題」として推理する。 ②2人が歩いた距離の和は、家から駅の距離の2倍である。 ③2人の間の距離は、1分あたりどれだけちぢまるか?出会い算と追いつき算の区別は、2つの物体(もしくは人物)の動く方向によって決まります 。 それぞれの内容を詳しくご紹介して行きましょう。 出会い算 出会い算は、 2つの物や人が向かい合って進み、出会うまでの時間や距離などを算出する問題です 。

旅人算 往復するときの解き方は 2回目に出会うときは 数スタ
出会い算 問題
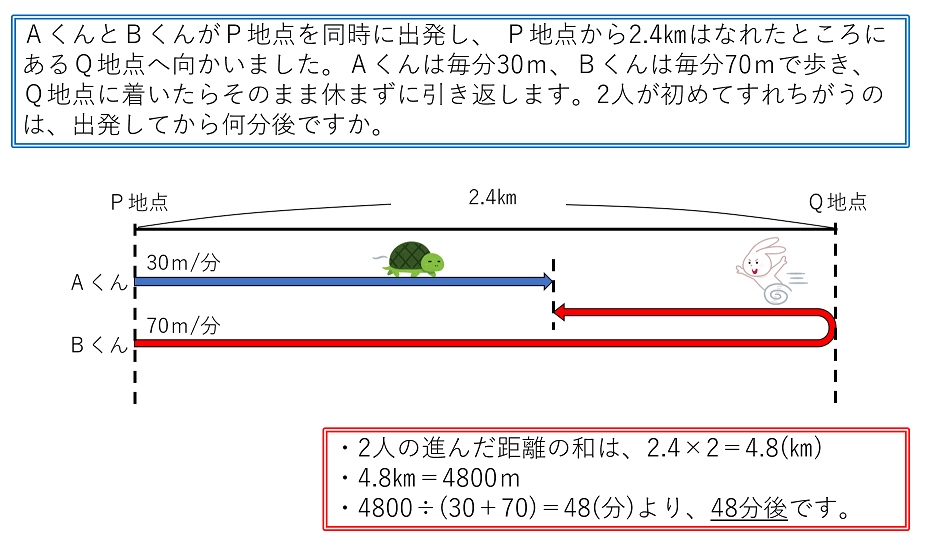
出会い算 問題-A 地点にいる太郎と,A 地点から600m 離れたB 地点にいる次郎が向かい合って同時に出発し,太郎は12 分おきに,次郎は15 分ごとに往復します。①練習問題 問題 A は分速80mで歩いて、家から1.5km離れた駅に向かって出発した。 A が出発してから12分後に B が自転車に乗って分速3mで A を追いかけた。 B は A に駅まであと何mのところで追いつくか求めなさい。 考え方 B が A に追いつく⇒2人




え こんなに簡単だったの 中学入試の分かりやすい旅人算の解き方 受験ボックス
70mで歩く人が、それぞれ�A,�B 7分 後に出会います。 70m/分150 m�ずつ近づくよって7分間の道のりは 150 × 7 = 1050 m� (2)時速50 kmで走る車と、時速両地点から向かい合って同時に出発すると、A,B間の距離をもとめなさい。 高頻出問題です。 一見難しそうですが、実は「受験算数」の出番は最後の小問のみです。 最初のセクションの「大問概要」を読んで、下準備をして挑みましょう。 速さ(小学6年生) 植木算(受験算数) 出会い算(受験算数)旅人算の基本パターン 速さの問題の中で、「登場人物が複数いる問題」を「旅人算」と呼びます。 登場人物が複数いることによって何が起こるかというと、「出会い」や「追いかけ」といったパターンの問題が生まれます。 最も王道なのは登場人物が2人
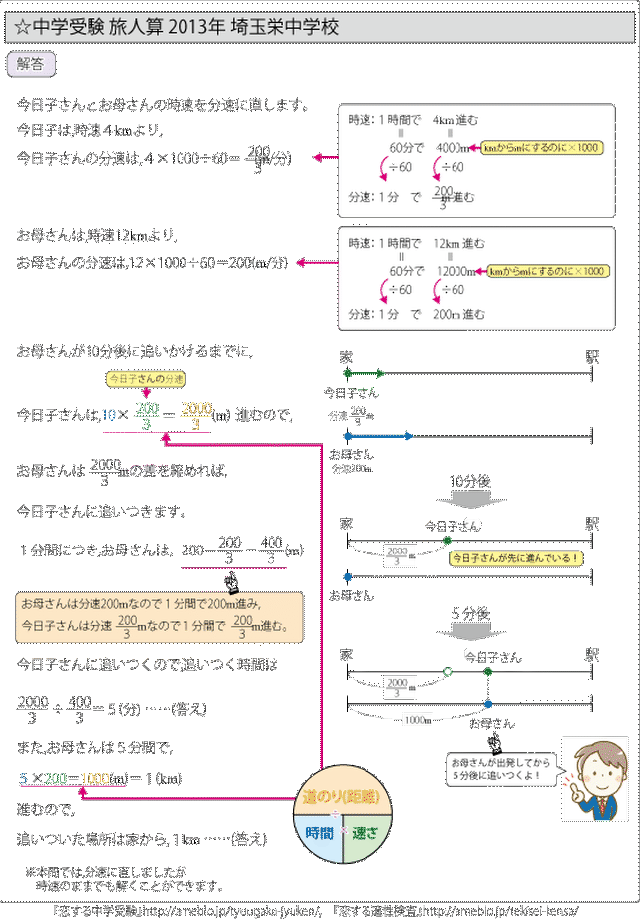
旅人算の2地点から出発して出会う出会い算の問題の解き方とコツ 2人が別々の地点を出発して向かい合って進む旅人算の問題です。 まずは問題文の内容をしっかり理解しましょう。 それでは早速例題をみていきます。 例題 A A 地点から B B 地点まで 32km出会いの旅人算<往復>(海城中 ①) 本日は、往復を繰り返す出会いの旅人算を扱います。 今回扱うものは、⑶を除けば、その単元の例題になっていそうな問題で、⑶も速さと比の話が分かっていればさほど苦労のない問題です。 難関校、中堅校旅人算(出会い算)の解説 旅人算(たびびとざん)は算数の速さを使った文章問題の形式で、2つの動くものがあり、その2つの速さと距離から出会うまでの時間を算出する計算のことを 出会い算 といいます。
小学校の算数でも 出会い算 として出題される問題です。 中学では方程式を使うことでこの問題を解きます。 出会ったときに2人が進んだ距離の合計は 問題文からポイントとなる箇所を抜き出します。 1周4.2km(4,0m) 兄分速160m 麻布中学校07年度 算数入試問題 旅人算 速さの出会いと追いかけ 解法1 A君はB君を15分ごとに追い越し・・・速さの追いかけ算(速さの差) B君はC君と2分ごとに出会います・・・速さの出会い算(速さの和) B君が7分かかって走る距離をC君は8分で走り出会い算 (であいざん)とは、 算数 の 文章題 の一つ。 旅人算 の1パターンで、2つの物がある2地点からある速さで向かい合って進む場合、何分後に出会うか、というのが基本パターンになる。



旅人算 往復経路 中学受験算数超特急シリーズ 無料版



印刷可能 中学受験 算数 速さ 旅人算
数学算数問題にチャレンジ 回答者地図帳 <答えを送っていただいた皆さんです> 令和3年7月 第262回出題 「出会い算の問題」 令和3年6月 第261回出題 「円周率の精度による結果の違い問題」 令和3年5月 第260回出題 「平面を分割する問題」 令和3年4月旅人算往復、2回目に出会うときの問題まとめ! お疲れ様でした! 往復を考える問題では、頭の中でのイメージが難しい なので、迷ったときには絵を描いて、2人が進んできた道のりがどういった値になっているのかを考えることが大事です。 数学・速さ出会い算が分かりません 『Aさんは毎分 m、Bさんは毎分 mの速さで、1キロ離れた場所から同時に歩き始めました。二人は何分後に出会うでしょう。』このような出会い算の問題が、わかりません。調べたら公式があるようで、『出会うまでの時間=2地点の距離÷速さの和



特殊算 旅人算編 首都圏 国立 私立中学校 受験対策 愛と魂を込めた テーマ別で市販の解説集よりよくわかる過去問題解説集 自宅でできる受験対策ショップ ワカルー Wakaru




旅人算の解き方まとめ 公式から応用問題3選までわかりやすい解説 中学受験算数 遊ぶ数学
旅人算ー出会いの問題 目標時間 名前 (1) m離れた2地点から 分速 mで歩く人と、分速 mで歩く人が、それぞれ A, B 両地点から向かい合って同時に出発します。2人は出発してから何分後に出会いますか。 A B m/分 m/分 ( )旅人算では2人の動きを把握することが第一歩! SPI・WEBテスト対策 作成日:15年05月24日 更新日:19年12月11日 ざっくり言うと 速さの問題の中でも頻出度は高め 旅人算を動画で解説! ポイントは2人の動きを把握すること セミナーに予約する シェア出会いました。2人が出会えたのは、Hello Schoolから何mはなれたところですか。 分後なので、そこから旅人算で考え 旅人算の解説ページ 練習問題




え こんなに簡単だったの 中学入試の分かりやすい旅人算の解き方 受験ボックス



中学受験 旅人算とは 基本公式から往復など応用問題 ダイヤグラムまで そうちゃ式 受験算数 2号館 図形 速さ
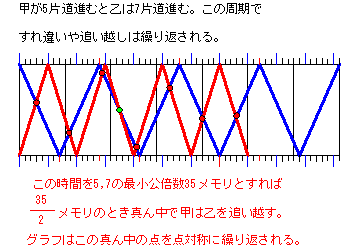
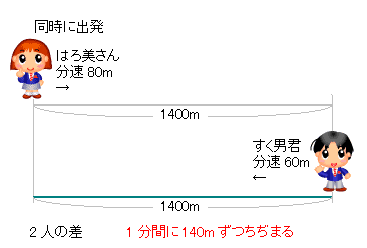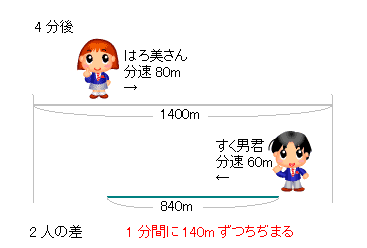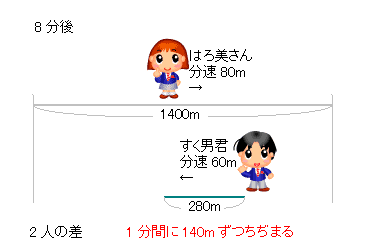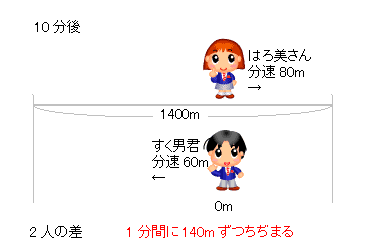
旅人算」の「出会い問題」とは、2つ以上の動く物体が同時に 離れた地点から向かい合って移動を開始する場合の推理法です。 すれちがう場合は、出あった時点で「さよなら問題」となり、 これが、「出会い・すれちがい問題」です。10分間でそれぞれ 10xm,10ymの道のりを歩く。 出会うときは2人の距離の和が1400mとなるので、10x10y = 1400 35分間でそれぞれ35xm,35ymの道のりを歩く。 A君がB君に追いつくのは2人の距離の差が1400mになるときなので 35x35y =1400 第9回 旅人算 77K 大人でもちょっと手こずってしまうような、難問奇問が続出する中学入試の算数。 でもだいじょうぶ、コツさえつかめば怖くありません! 学習サポートセンターのカズが、算数を楽しく学ぶ方法を伝授します。 更新 6年




中学受験 算数 12月 差集め算 旅人算 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ




中学受験算数 出会い算 旅人算 超初級講座 アニメーションでわかる Ok算数 8分間 Youtube
はじめに 今回は旅人算(出会い算・追いつき算)に関して詳しく解説します。 速度に関する基本的な計算に関しては深く理解出来ている前提となります。まずはその部分を詳しくお知りになりたい方は、本ブログの別記事(コチラ)をご参照下さい。 では、解説を始めます。 出会い算 例 #出会い算 #問題 <お悩み> spiや公務員試験に出る「旅人算」特に、「出会い算」と呼ばれる、速さの問題が難しいと考えている方。 受験をするとき、できるだけ時間をかけず、本質をおさえ、効率的に解きたい。 こういった疑問にお答えします。 こんにちは、ウチダです。 今日は中学受験算数講座第4回として 「旅人算」 について詳しく見ていきたいと思います。 旅人算の基本は「出会い算」「追いつき算」の $2$ つについてある共通点を見出すことです。 その共通点を見つけることで、今回用意した応用問題 $3$ つもかなり解き
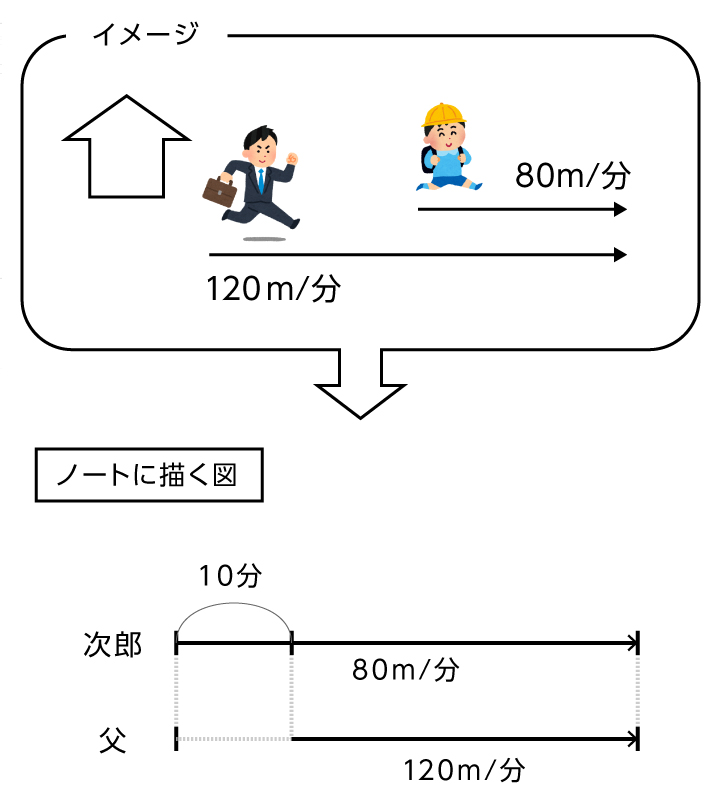



旅人算ってどんなもの 旅人算をわかりやすく解説 中学受験ナビ




グラフが登場する旅人算の解き方を問題集形式でご紹介
今月の問題 回答者地図帳 <答えを送っていただいた皆さんです> 令和3年7月 第262回出題 「出会い算の問題」 令和3年6月 第261回出題 「円周率の精度による結果の違い問題」 令和3年5月 第260回出題 「平面を分割する問題」 時計算とは? 時計の長針(1時間に360度・1周)と短針(12時間で360度・1時間で30度) が作る角度やその他(重なる時とか一直線になる時)を問う問題です。 時計算は、時計の長針と短針を使った「旅人算」と考えられます 。出会い算の変則的な問題です。 はじめて解くタイプの問題で解き方の方針が分からなくても、図に書いて整理すれば自然と解き方が見えてくると思います。 解法は主に2つあるのでそれぞれ見ていきましょう。 解法1
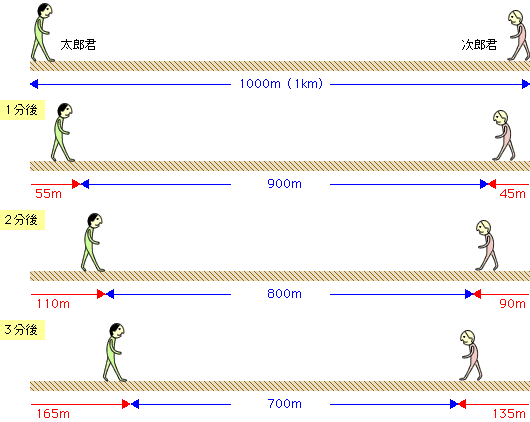



旅人算 算数の教え上手 学びの場 Com
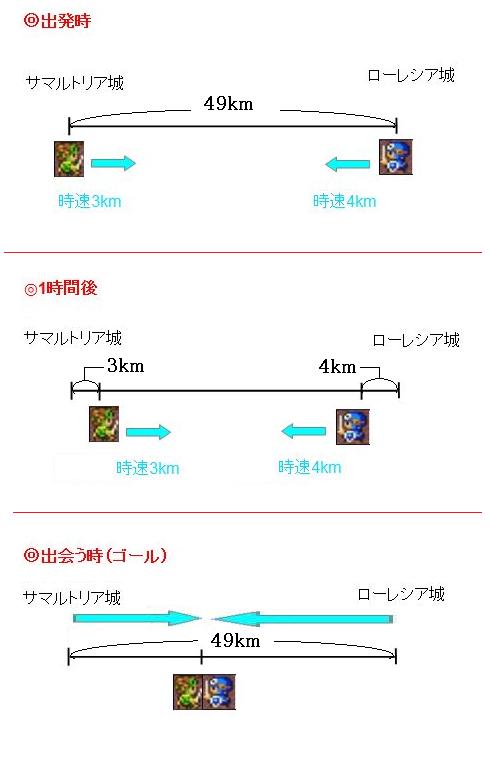



旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける
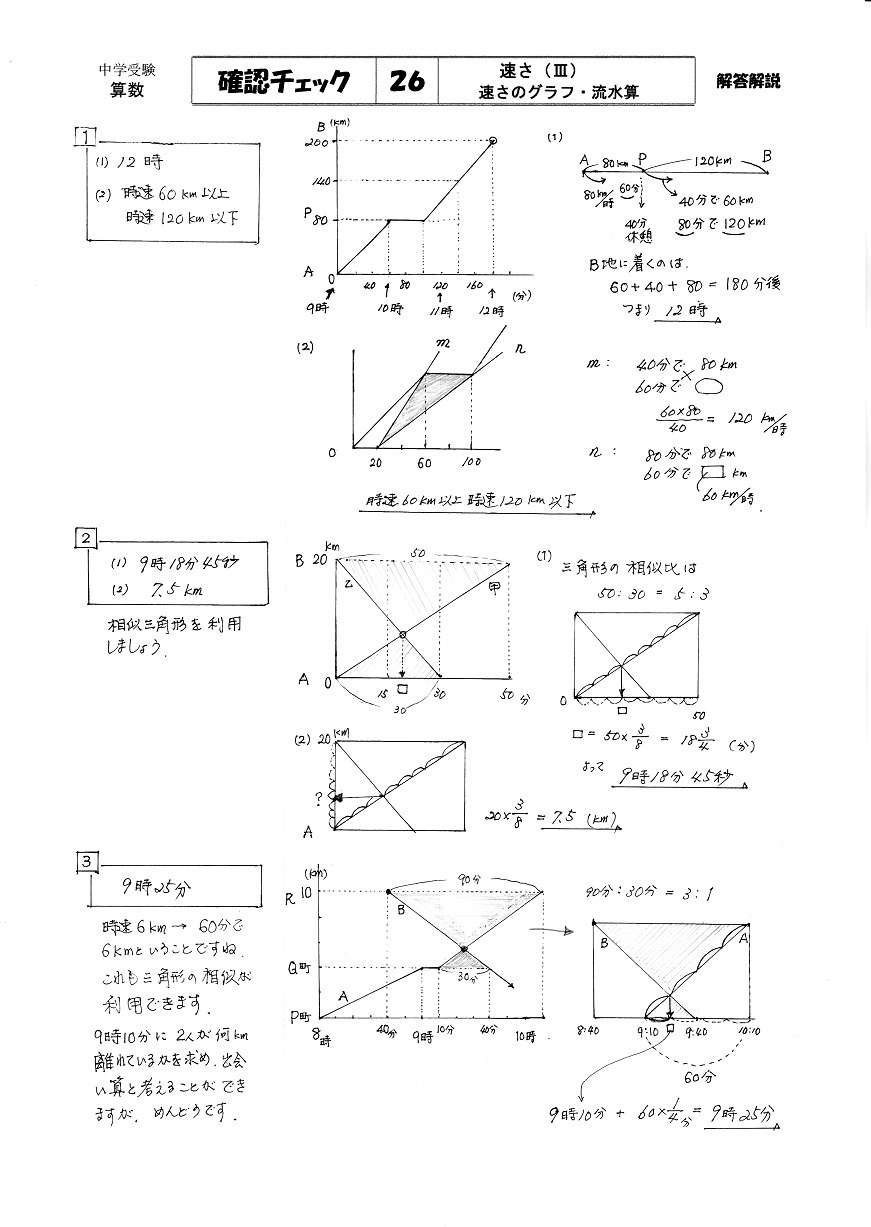



中学受験 算数確認チェック26 速さ 速さのグラフ 流水算 グランパは元塾長




中学受験5年の壁 点の移動 攻略法を完全公開 たぶお Sapix サピックス A1 養成講座




え こんなに簡単だったの 中学入試の分かりやすい旅人算の解き方 受験ボックス
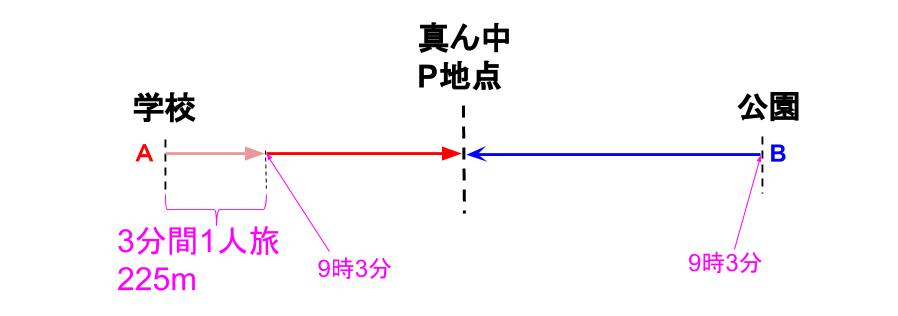



速さ 旅人算の応用 その3 中学受験算数の家庭学習教材 カンガループリント
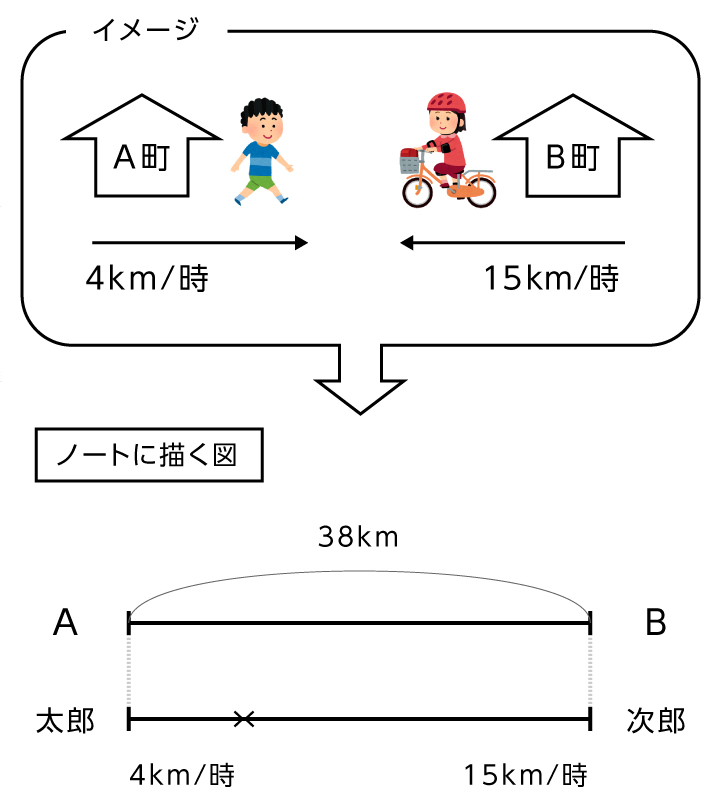



旅人算ってどんなもの 旅人算をわかりやすく解説 中学受験ナビ
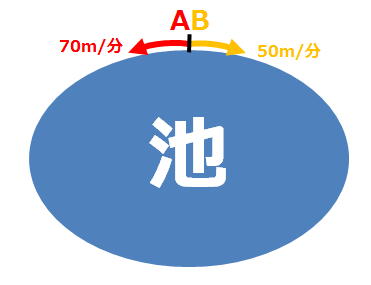



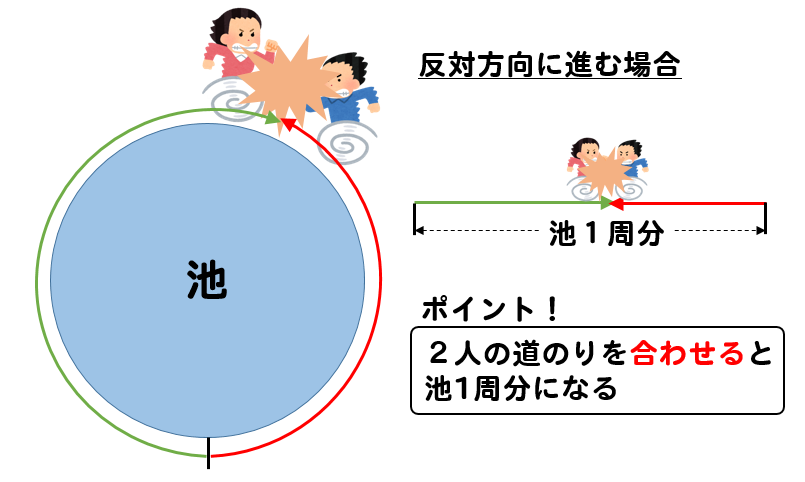
旅人算 池の周りを回る二人が出会う問題 の解き方



佐賀県 中学受験の対策 特殊算とは何か 家庭教師のトライ 佐賀県 エリアブログ



旅人算 出会い問題 すれちがい問題




旅人算 往復するときの解き方は 2回目に出会うときは 数スタ
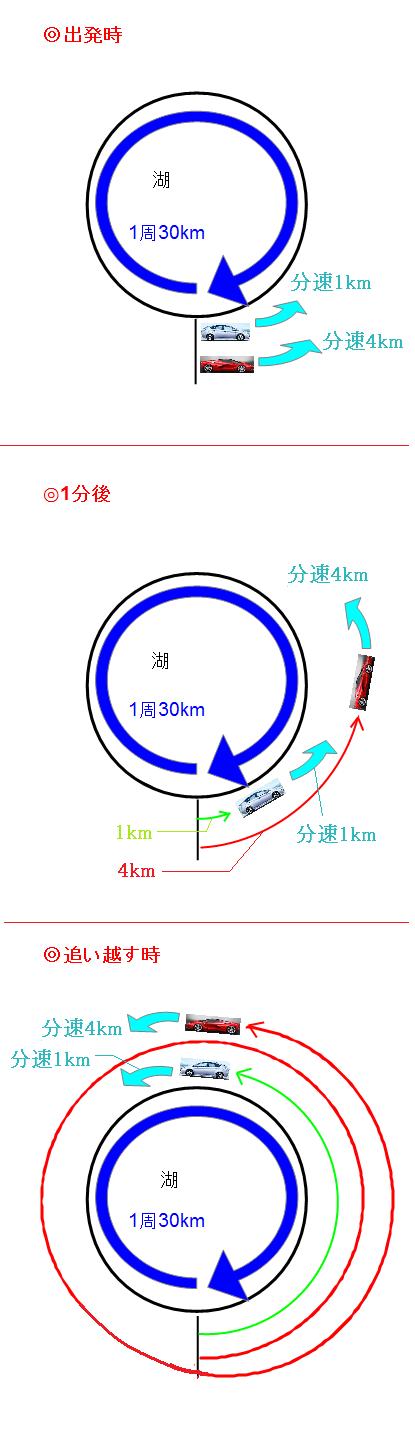



旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける




算数文章題講座 旅人算の解き方 基本問題
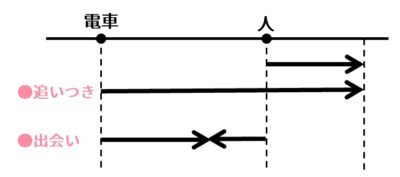



中学受験算数 出会いと追いつきの旅人算の問題 Stupedia
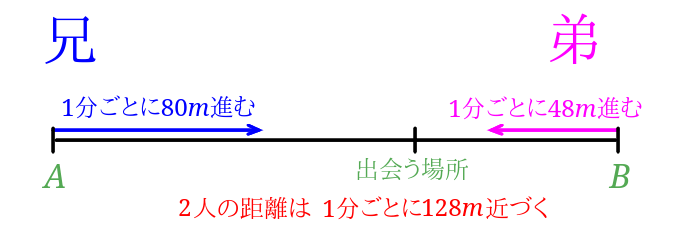



旅人算の苦手を克服 分かりやすく教える方法と解き方はコレ みけねこ小学校
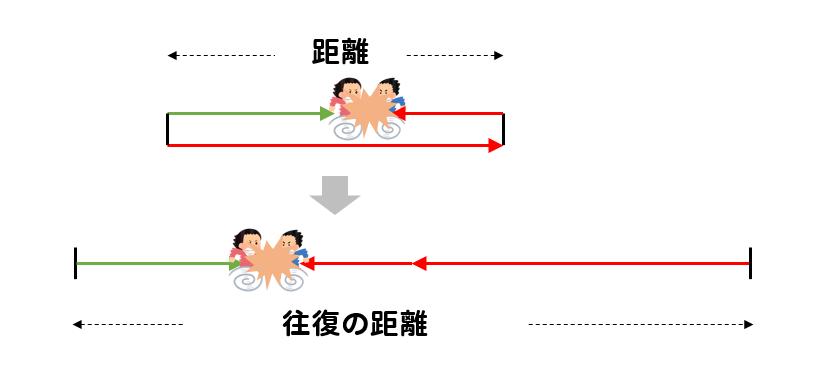



旅人算 往復するときの解き方は 2回目に出会うときは 数スタ




Spi中級上級編 18章 速度 旅人算 出会い算 池 湖の問題 Youtube




公務員試験 数的推理 旅人算 吉武瞳言のウェブ講座 Youtube




旅人算 Wikipedia




旅人算の問題と解き方その1 2人が 分後に出会う Irohabook



1




旅人算の解き方まとめ 公式から応用問題3選までわかりやすい解説 中学受験算数 遊ぶ数学



旅人算 解けるかな 算数の難問に挑戦




旅人算の解き方まとめ 公式から応用問題3選までわかりやすい解説 中学受験算数 遊ぶ数学




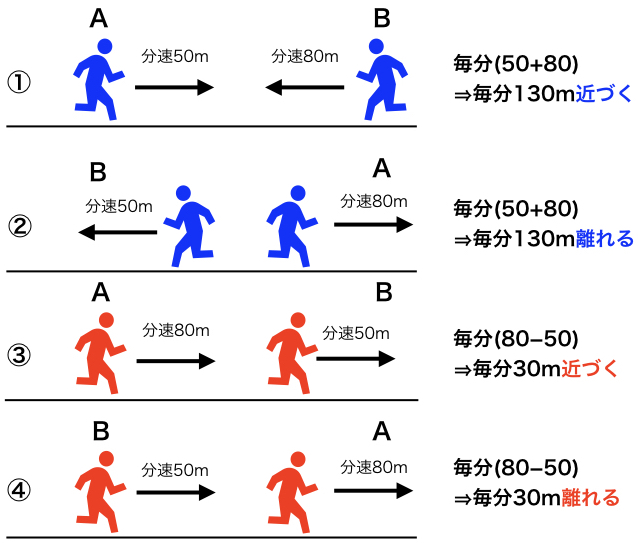
旅人算 速さの和と差から出会い算と追い越し算を再考する みみずく戦略室



中学受験算数 旅人算 Z1ztpytmx0 算数問題集のアキラストア 通販 Yahoo ショッピング



旅人算の練習問題と解説 みけねこ小学校




中学数学 方程式 旅人算 追いつく Youtube
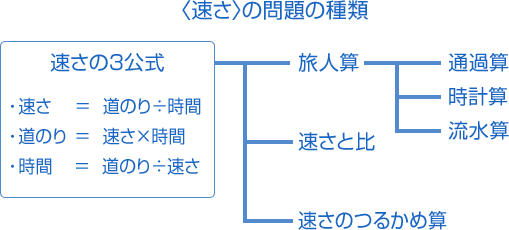



算数 速さ 旅人算 通過算 中学受験 ベネッセ教育情報サイト




旅人算の解き方まとめ 公式から応用問題3選までわかりやすい解説 中学受験算数 遊ぶ数学




印刷可能 中学受験 算数 速さ 旅人算



Http Www Chugakujuken Com Pdf Data Up San 11 1 Pdf




灘中解説速報 年第3問 旅人算と比 算数星人のweb問題集 中学受験算数の問題に挑戦
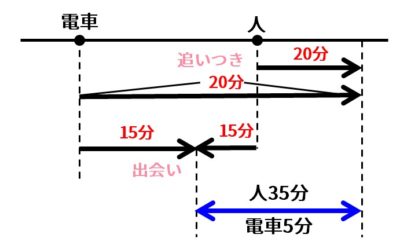



中学受験算数 出会いと追いつきの旅人算の問題 Stupedia
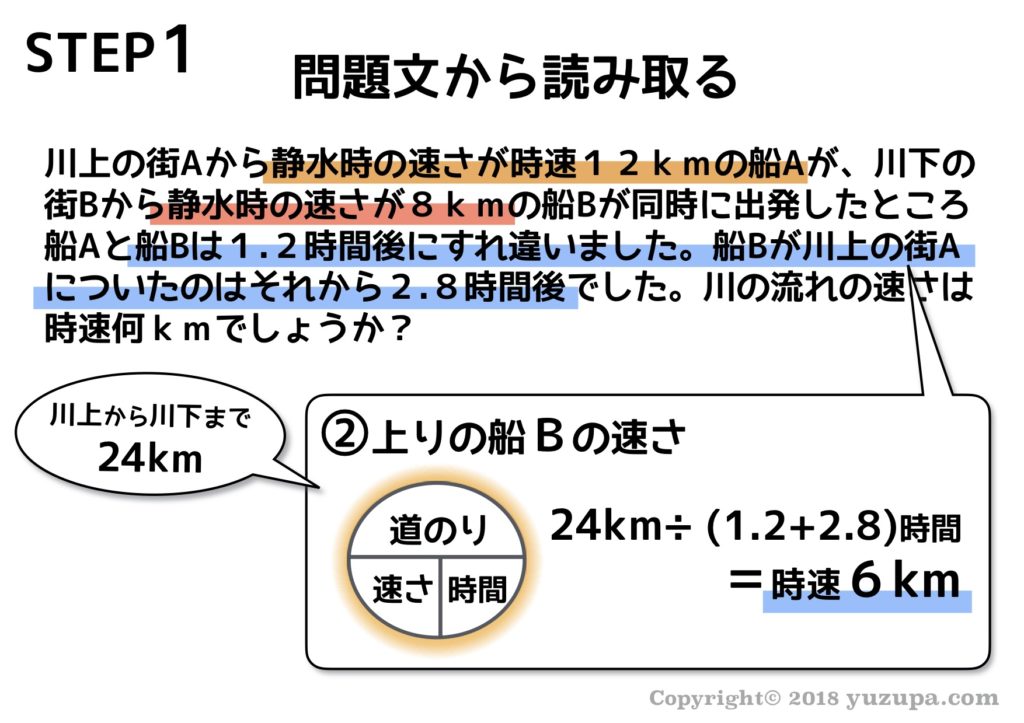



中学受験 流水算は 4つ速さを整理すれば簡単に解ける かるび勉強部屋




旅人算の基本 図をかいて整理しよう



出会う旅人算の解き方 考え方 算数パラダイス
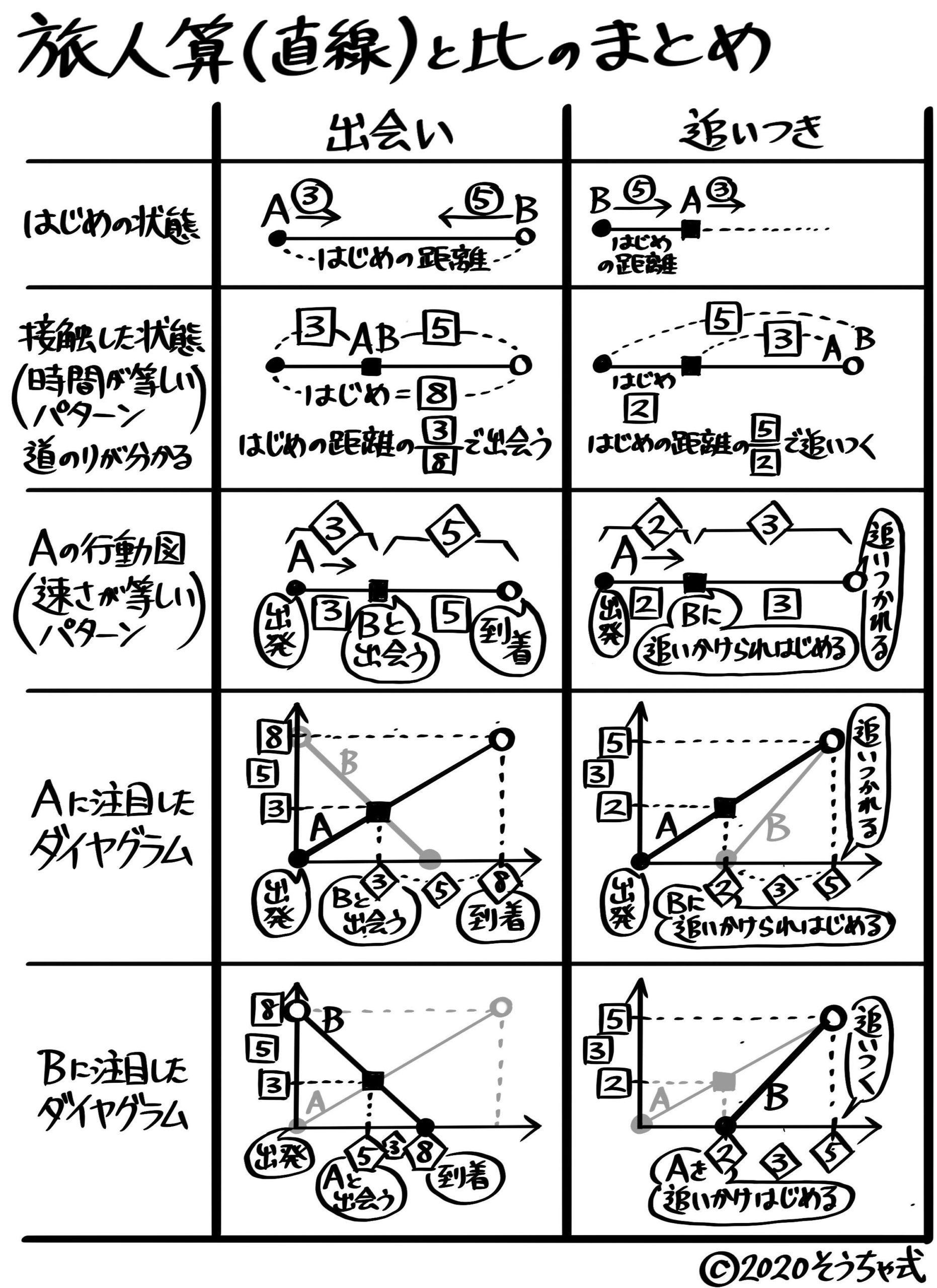



作成中 中学受験 速さ 旅人算と比のまとめ 出会い 追いつき 往復 そうちゃ式 受験算数 2号館 図形 速さ




算数文章題講座 旅人算の解き方 基本問題
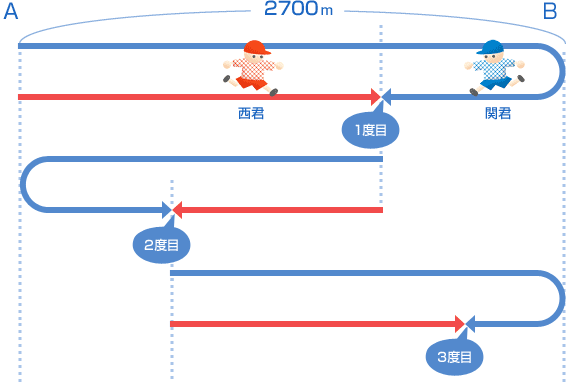



算数 速さ 旅人算 通過算 中学受験 ベネッセ教育情報サイト




旅人算の解き方まとめ 公式から応用問題3選までわかりやすい解説 中学受験算数 遊ぶ数学
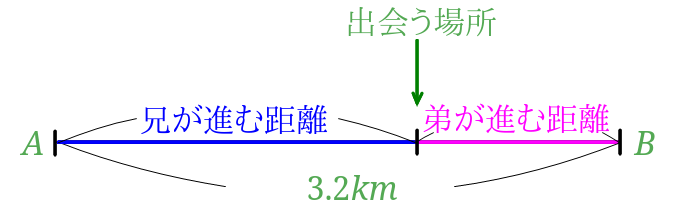



旅人算の苦手を克服 分かりやすく教える方法と解き方はコレ みけねこ小学校




旅人算 2人が追いつく問題の解き方は 数スタ




例題あり 旅人算とは 出会い算 追いつき算など種類別の解き方や教え方のコツも解説 学びtimes



1




算数文章題講座 旅人算の解き方 基本問題




慶應義塾普通部13年度算数入試問題5 旅人算 中学受験から医学部受験までプロにお任せ プロ家庭教師集団スペースone 公式




中学受験算数 実力チェック 29速さと比 旅人 通過算 グランパは元塾長



3




旅人算 の問題の解き方 小学生に教えるための分かりやすい解説 数学fun



3人旅人算 Wikipedia




甲陽学院中2019年 旅人算ー 中学受験算数の良問 難問 基本問題
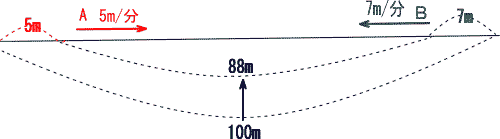



算数の特殊算 旅人算 速さの出会い算 解説桜蔭中学校07年度算数入試問題 医学部受験ならプロ家庭教師集団スペースone 公式 中学受験から対応




旅人算の基本 図をかいて整理しよう




旅人算 の問題の解き方 小学生に教えるための分かりやすい解説 数学fun




旅人算の解き方まとめ 公式から応用問題3選までわかりやすい解説 中学受験算数 遊ぶ数学




2次方程式の文章題 出会い算 制限3分 中学数学 理科 寺子屋塾の復習サイト
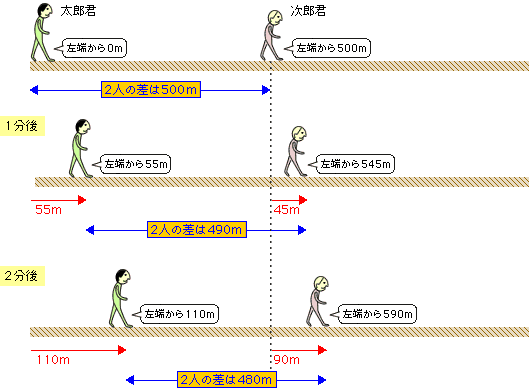



旅人算 算数の教え上手 学びの場 Com



旅人算 問題の解説まとめ それぞれのパターンの解き方は 数スタ




旅人算の基本 図をかいて整理しよう



旅人算 わかりやすい出会い算と追いつき算の解き方を簡単計算 Landgather




旅人算の基本 図をかいて整理しよう




旅人算 の問題の解き方 小学生に教えるための分かりやすい解説 数学fun
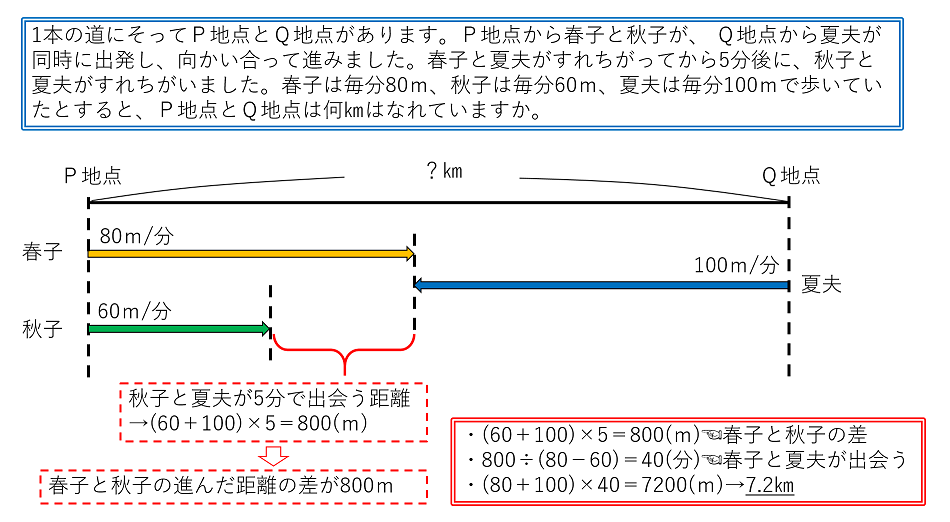



印刷可能 中学受験 算数 速さ 旅人算




旅人算と比 中学受験の算数 理科ヘクトパスカル




旅人算 問題の解説まとめ それぞれのパターンの解き方は 数スタ




中学受験算数 出会いと追いつきの旅人算の問題 Stupedia




高槻中2020年 旅人算ー 中学受験算数の良問 難問 基本問題




旅人算




旅人算 の文章問題 計算ドリル 問題集 数学fun
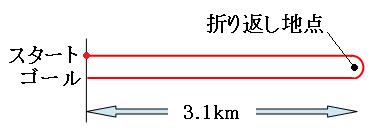



旅人算の練習問題 標準編 文章をよく読めば大丈夫



旅人算の応用変化 第一変化 折り返し問題




旅人算 基本 中学受験準備のための学習ドリル




Spi中級上級編 18章 速度 旅人算 出会い算 追いつき算コラボ Youtube




算数文章題講座 旅人算の解き方 基本問題




旅人算 の問題の解き方 小学生に教えるための分かりやすい解説 数学fun




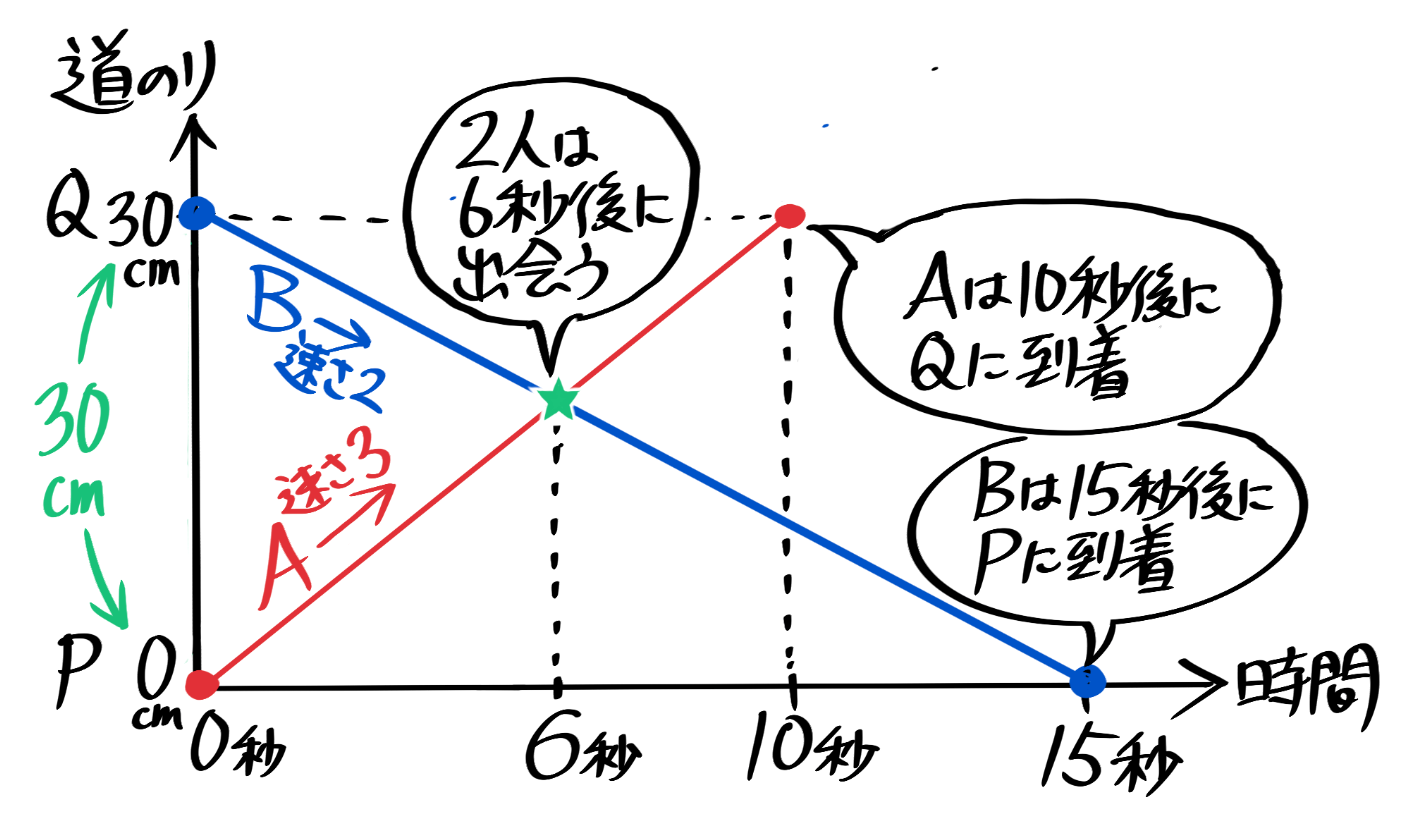
解説動画付 予習シリーズ5年生 算数 上no18 旅人算とグラフ 1 のおはなし 中学受験コベツバ
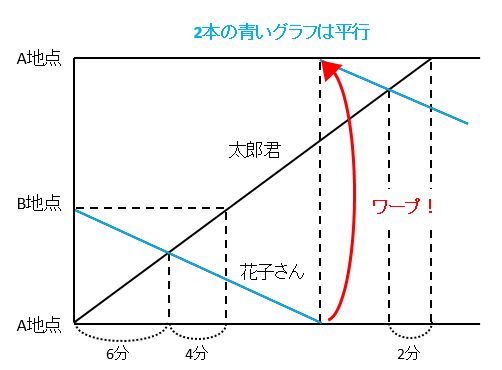



速さと比 ダイヤグラムで旅人算を図形的に考える 応用編 みみずく戦略室




え こんなに簡単だったの 中学入試の分かりやすい旅人算の解き方 受験ボックス
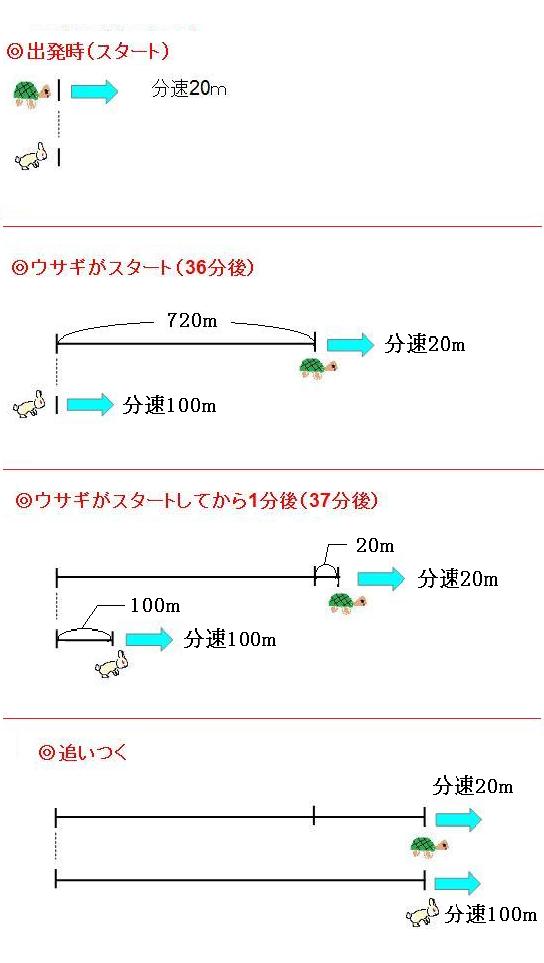



旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける
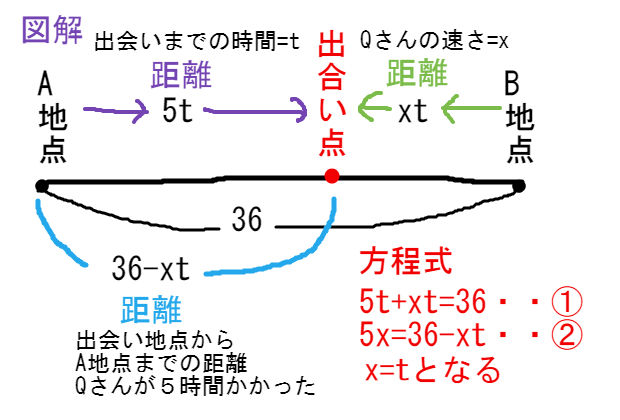



2次方程式の文章題 出会い算 制限3分 中学数学 理科 寺子屋塾の復習サイト
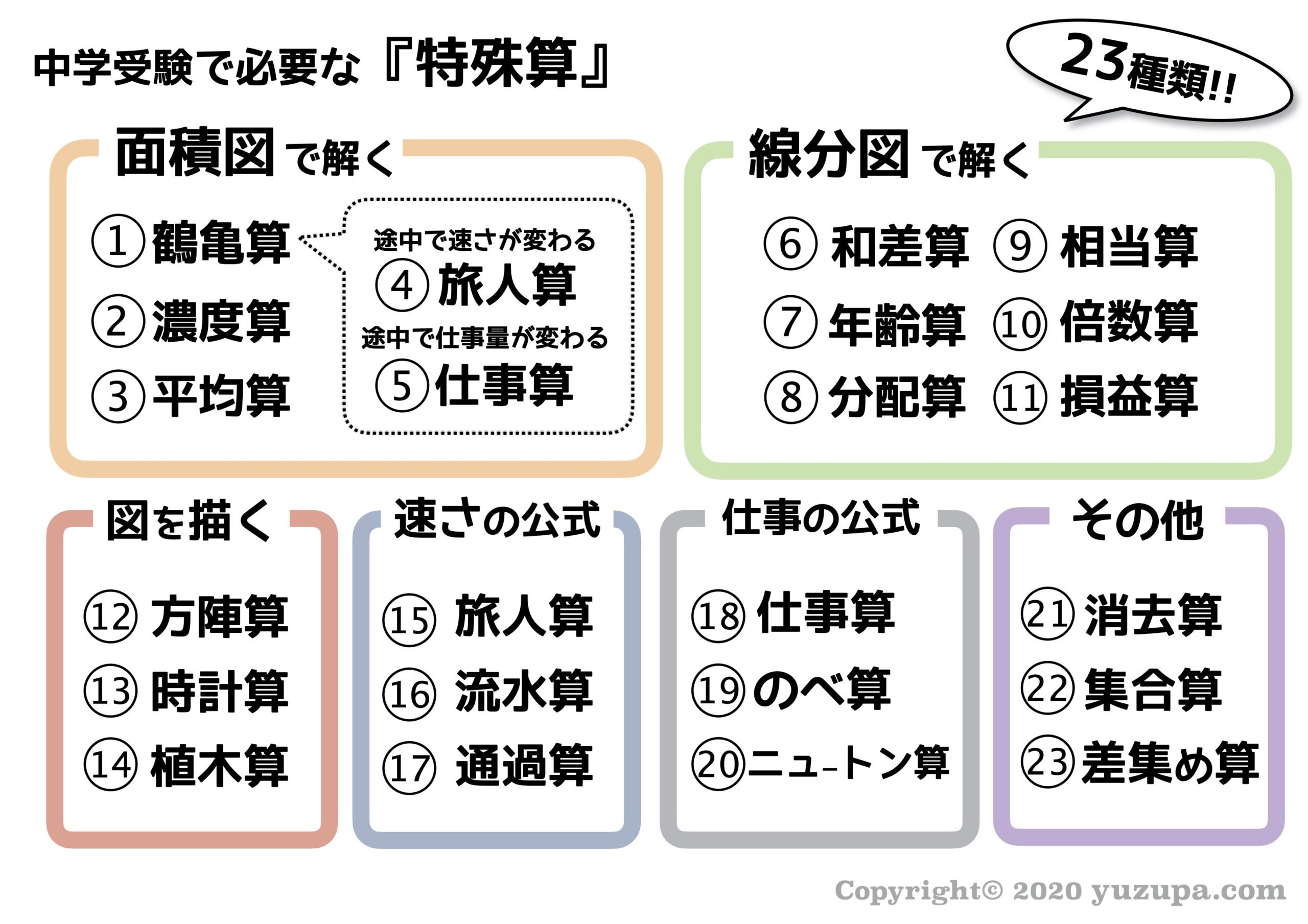



中学受験 特殊算は何種類ある 算数の文章題の見分け方 かるび勉強部屋



旅人算




3人の旅人算 考え方と解き方



旅人算の応用変化 第三変化 ダブル旅人算
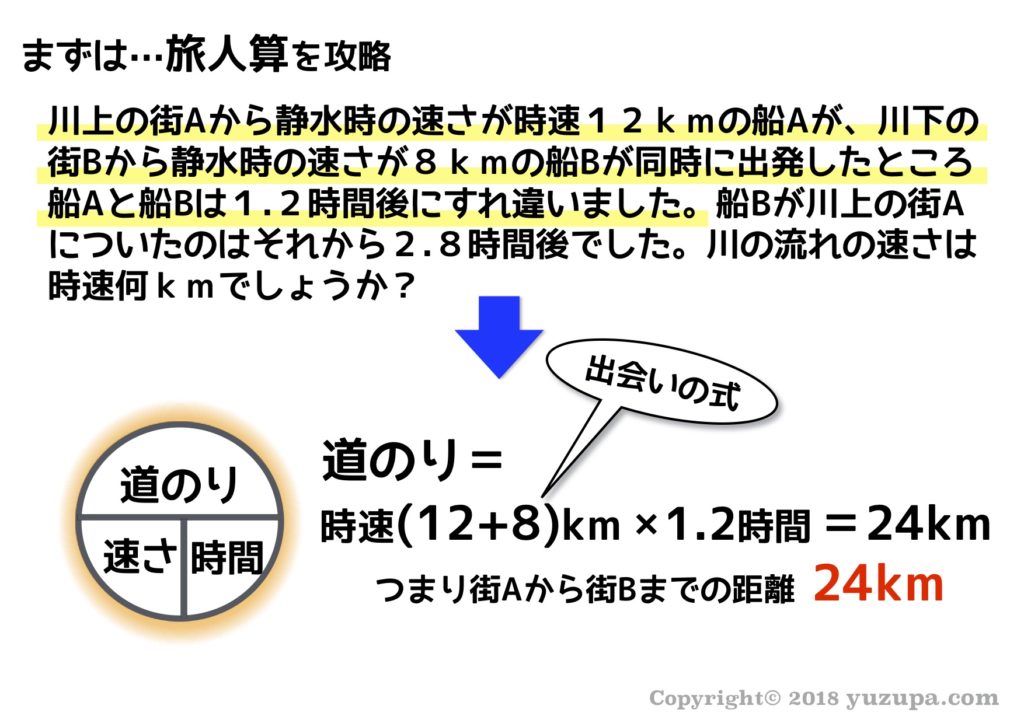



中学受験 流水算は 4つ速さを整理すれば簡単に解ける かるび勉強部屋




旅人算 池の周りで出会う問題の解き方 考え方 算数パラダイス
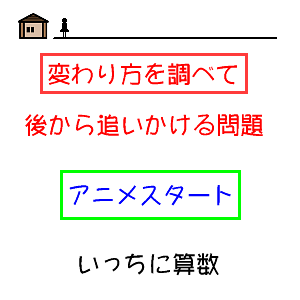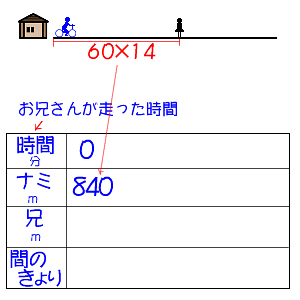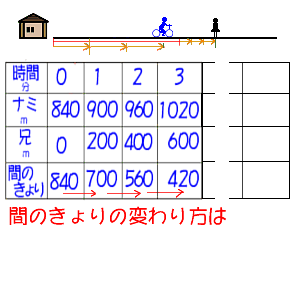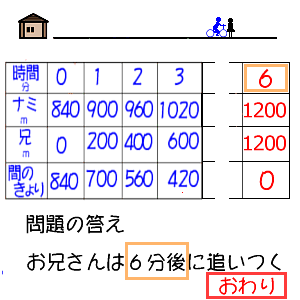



6年算数 変わり方を調べて 1 出会い算
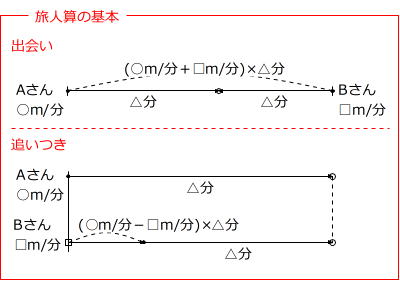



第492回 合否を分ける問題の解き方 旅人算 前田昌宏の中学受験が楽しくなる算数塾



1次方程式 速さ 中学から数学だいすき




旅人算の基本 図をかいて整理しよう



Math 中学受験 旅人算 発展問題 働きアリ




旅人算の解き方まとめ 公式から応用問題3選までわかりやすい解説 中学受験算数 遊ぶ数学



1



0 件のコメント:
コメントを投稿