円錐に関する問題への速答 必須知識 中学 数学 理科の復習サイト
円錐定義は後述をある平面で切断したときに切断面に現れる曲線を総称して円錐曲線という。 円錐曲線には楕円，円，放物線，双曲線がある。 (1) メナイクモス 円錐曲線はメナイクモス( M enaiqmoc (Menaichmos ，Menaechmus) BC4 世紀) によって発見さ れたといわれている。 問題 図のように，長さ l の軽くて伸びない糸の一端を固定し，他端に質量 m の物体をとりつけ，速さ v で円錐振り子運動させる．物体が運動する平面は水平面に平行であり，物体は鉛直線から角度 θ を保ちながら円運動している．重力加速度の大きさを g
円錐 問題 表面積
円錐 問題 表面積- というわけで、今回の記事では円錐の表面積を簡単に求める方法について解説していくよ！ どのような考え方を用いているのか。 どのような計算をすればよいのか。 更には、練習問題を通して理解を深めていきましょう。問題 下の図のように、底面の半径が \(28cm\),母線の長さが \(100cm\) の円錐に \(2\) つの球が内接しています。球と球も接しています。 このとき、小さい球の半径を求めなさい。 解説 円錐と内接球・そ
相似の問題 テスト 受験対策 苦手な数学を簡単に
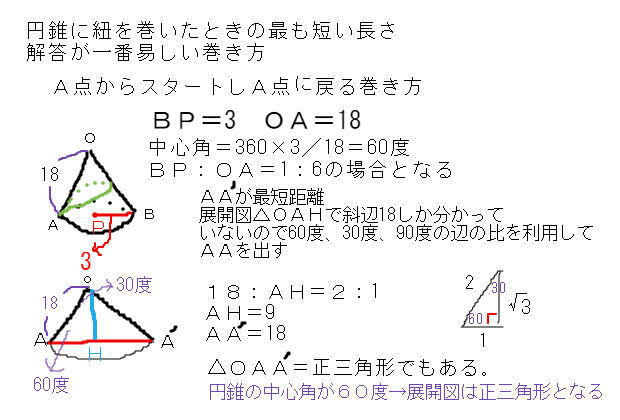
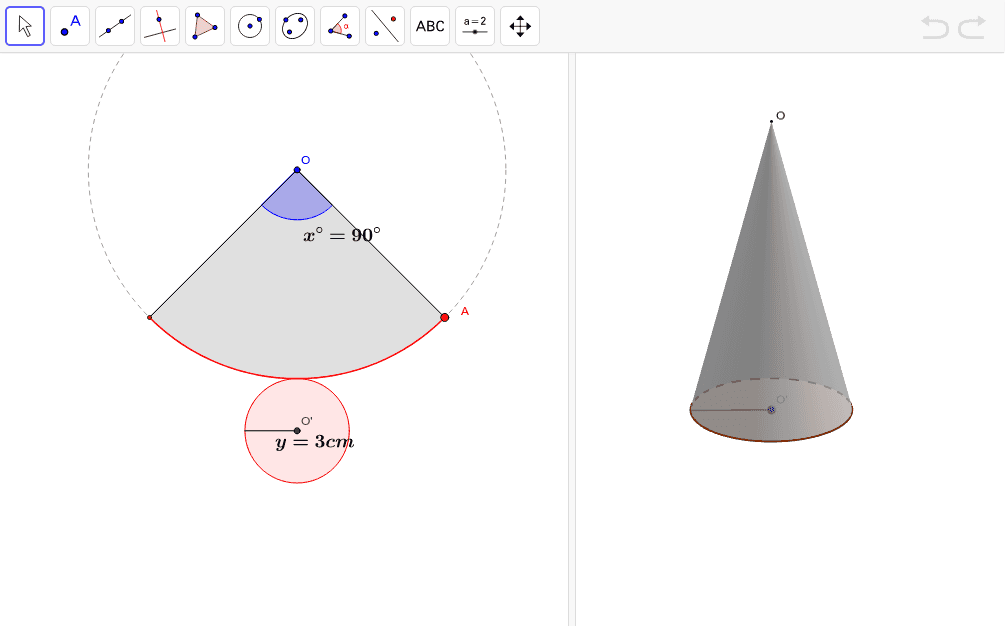
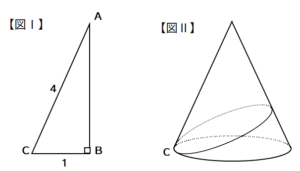
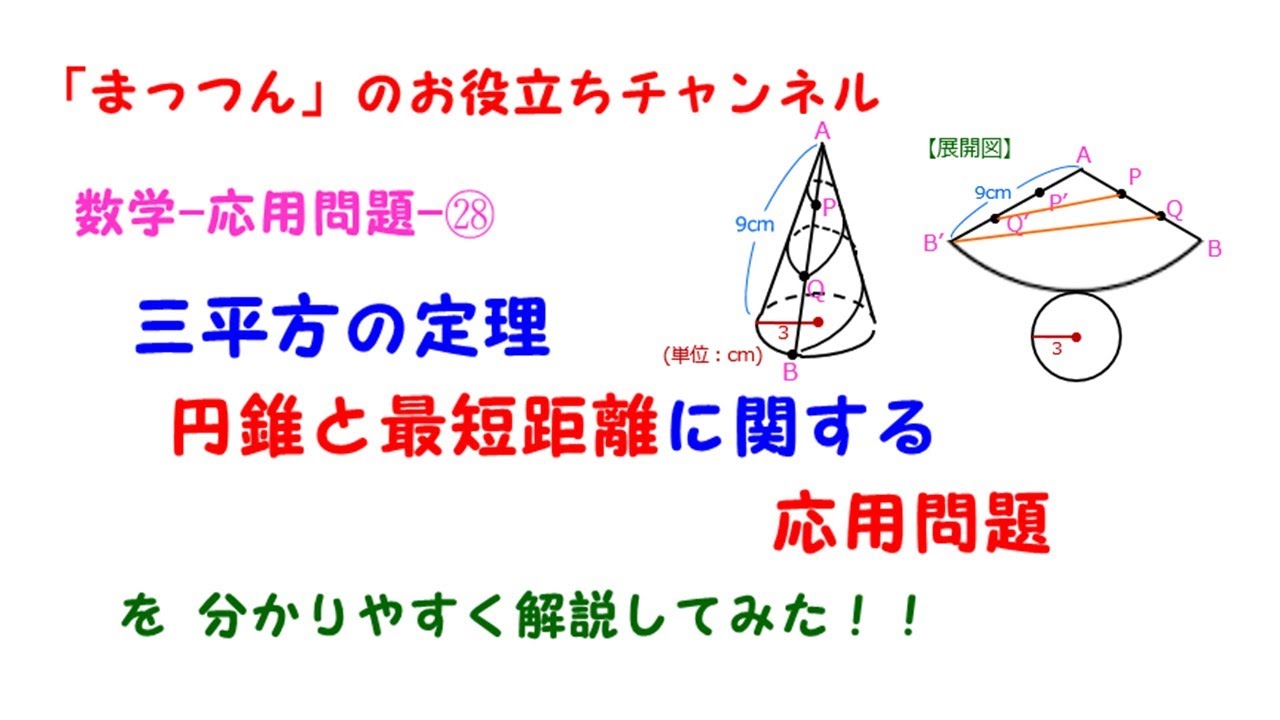
規則性の問題の出題パターン3選！ 算数 2218 国府台女子学院中等部－19年度算数大問2(1)分配算－過去問解説 算数 まずは のある計算に慣れるところから始めよう！還元算・相当算の解き方初 ひもの問題は展開図を書いて、ひもが直線になればよい。 （1）展開図をかく。 以下のような図を書く。 （必要なとこだけ） すると、線分CDを求めればよいことがわかる。 ここでおうぎ形の角度に注目する。 （角度がわかれば三平方の定理が使えるから） おうぎ形の弧の長さは中心角をaとすると、 30× 2× π× a 360 30 × 2 × π × a 360 ・・・ また、弧の長さは円周と同じなのでしかし円錐の場合、側面は扇形となりますが中心角は問題文で与えられないので少し複雑です。 なので円錐の側面積についてもう少し解説していきます。 円錐の側面積の求め方 側面積は扇形なので、扇形の面積の公式を書き出しましょう。
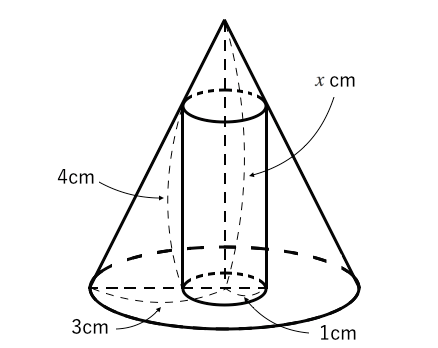
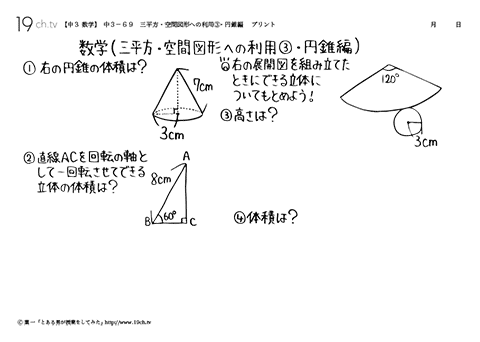
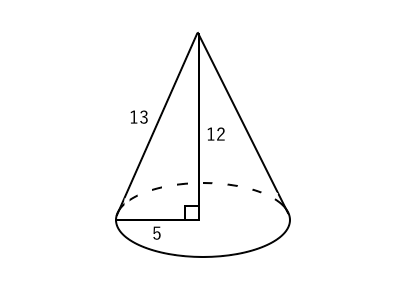
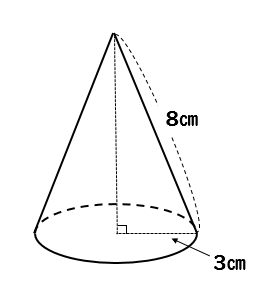
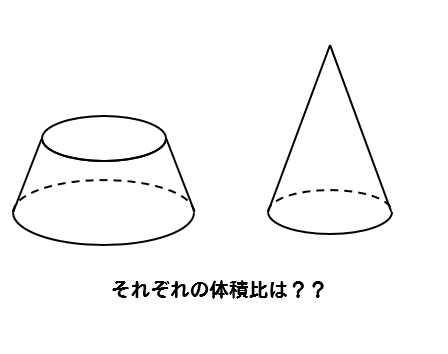
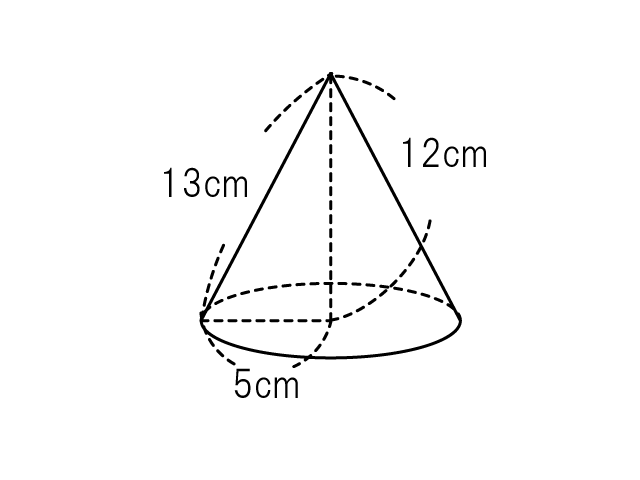
円錐の体積を求める計算問題 底面の半径と高さから体積を求める問題 底面の半径 2、高さ 3 の円錐の体積 V を求めよ。 円錐の体積の公式に代入すればいいだけですね。 V = 1 3πr2h = 1 3π× 22 × 3 = 4π V = 1 3 π r 2 h = 1 3 π × 2 2 × 3 = 4 π 円錐台の体積を求める問題 下図のように、底面の半径 4、高さ 6 の円錐を、高さ 3 の点を通り底面に平行な平面で切った図形がある（円錐台）。 この立体の上底 上図のように半頂角が θ の円錐容器を円錐の頂点を水平面に固定し，円錐容器の底面が水平面と平行になるようにした．次に，質量 m の物体を円錐容器の内部で角速度 ω の等速円運動をさせた．円軌道の面は水平面と平行にあり，水平面から円軌道面まで発展円すいの体積を求める問題 問題3 図の円すいの体積を求めなさい。 問題の見方 問題2と同じように， (底面積)× (高さ)×\frac {1} {3}= (体積) (底面積) × (高さ) × 31 = (体積) で求めたいのですが， (高さ)がわかりません。 いったいどうすればよいでしょうか？ ポイントになるのは 三平方の定理 (中学3年生で学習) です。 直角三角形の三辺をa，b，c (cは斜辺)とするとき，三平方の定理より，
円錐 問題 表面積のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 立方体の倍積問題 | 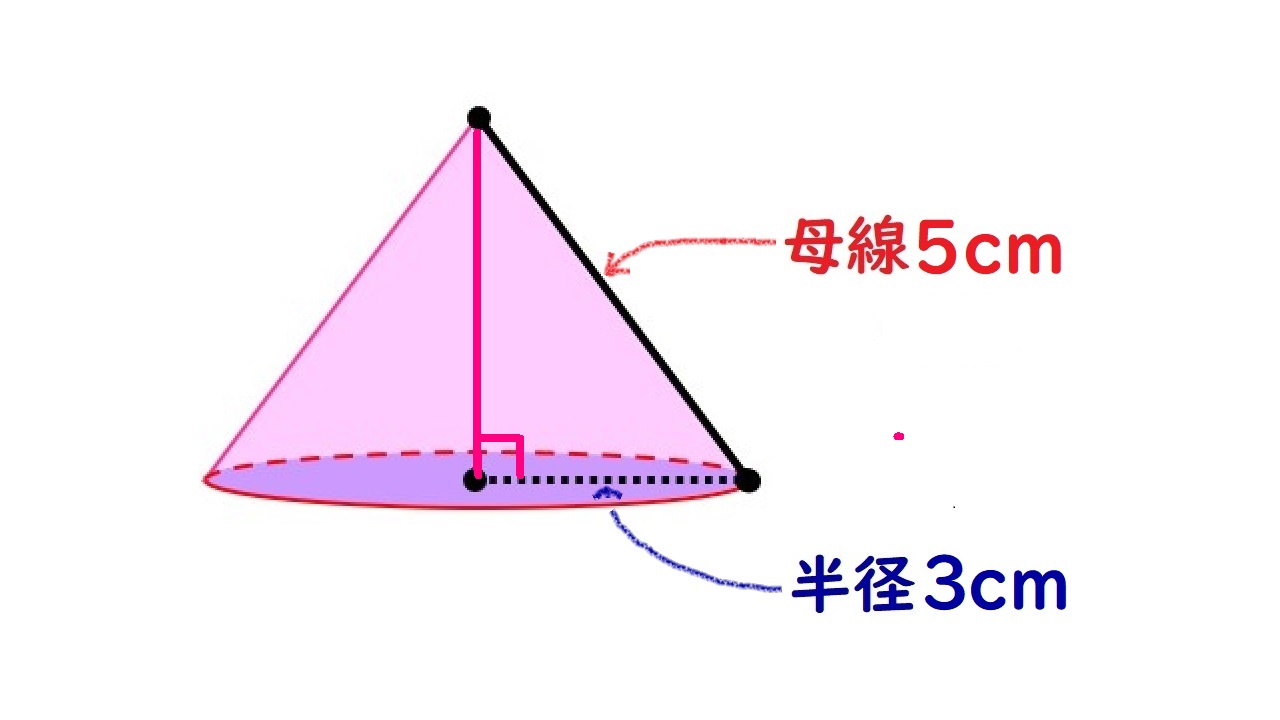 立方体の倍積問題 |  立方体の倍積問題 |
 立方体の倍積問題 |  立方体の倍積問題 |  立方体の倍積問題 |
 立方体の倍積問題 |  立方体の倍積問題 |  立方体の倍積問題 |
「円錐 問題 表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 立方体の倍積問題 |  立方体の倍積問題 |  立方体の倍積問題 |
 立方体の倍積問題 |  立方体の倍積問題 |  立方体の倍積問題 |
 立方体の倍積問題 |  立方体の倍積問題 | 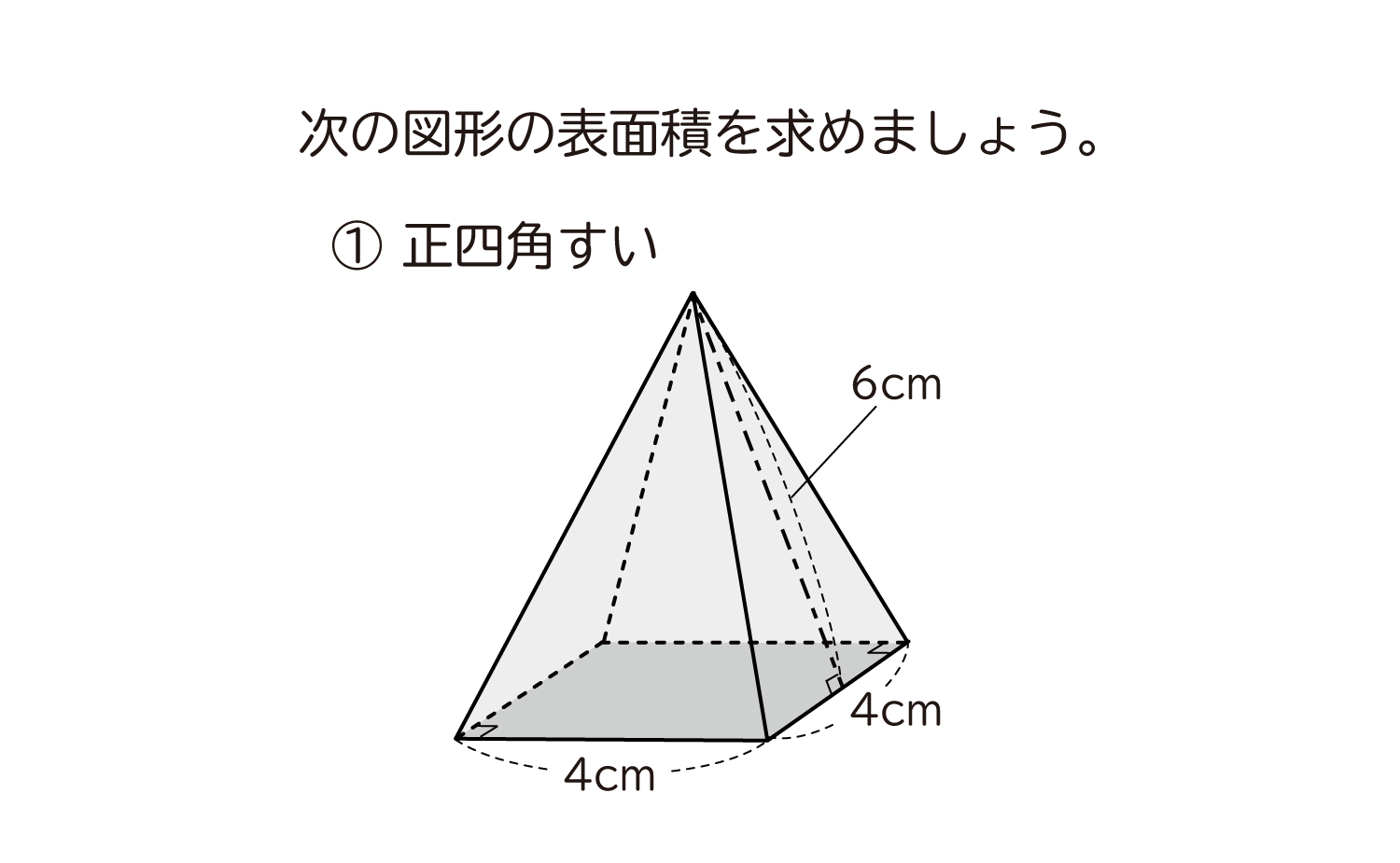 立方体の倍積問題 |
「円錐 問題 表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 立方体の倍積問題 | 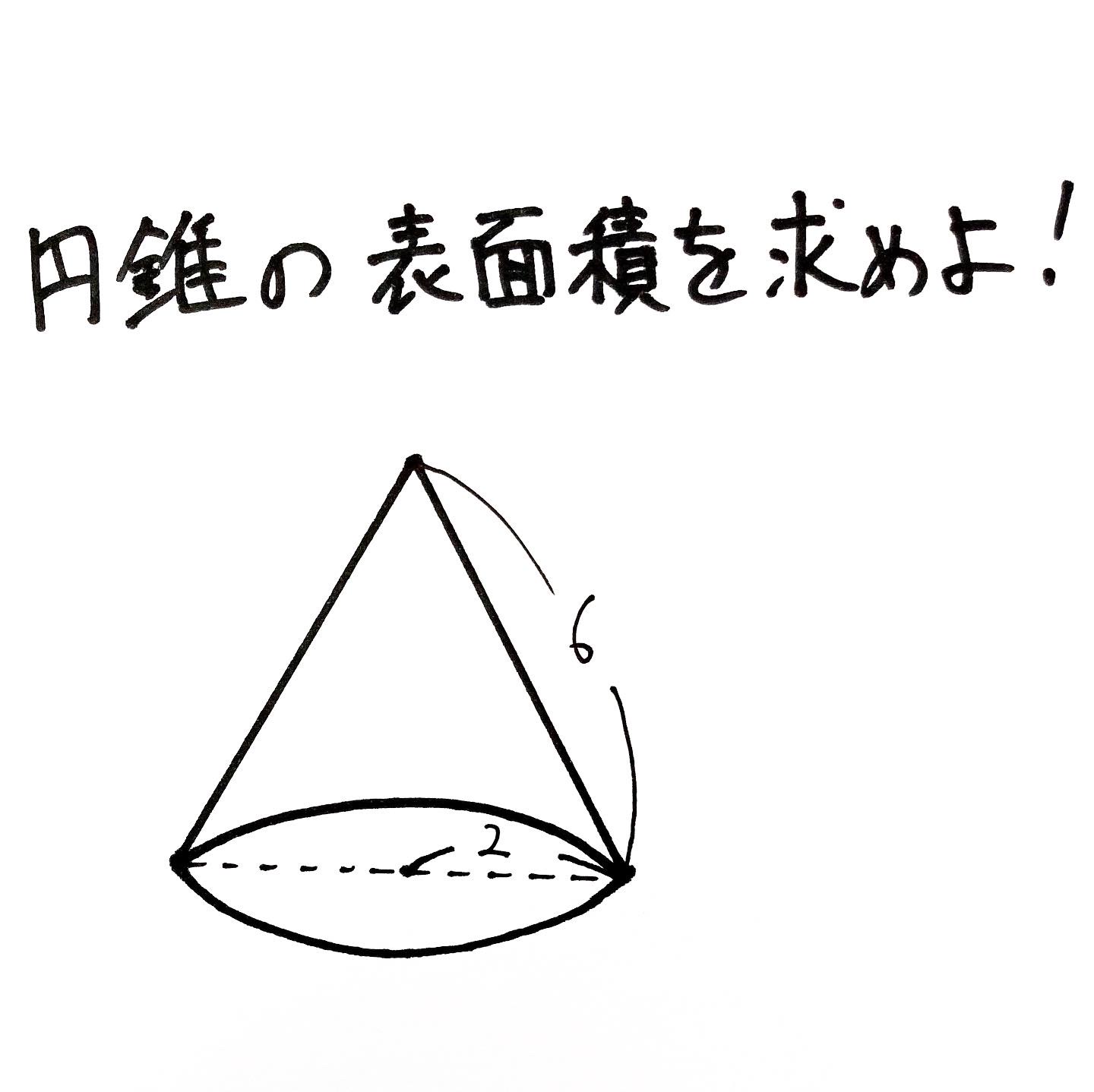 立方体の倍積問題 |  立方体の倍積問題 |
 立方体の倍積問題 |  立方体の倍積問題 |  立方体の倍積問題 |
 立方体の倍積問題 |  立方体の倍積問題 |  立方体の倍積問題 |
「円錐 問題 表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 立方体の倍積問題 |  立方体の倍積問題 |  立方体の倍積問題 |
 立方体の倍積問題 |  立方体の倍積問題 |  立方体の倍積問題 |
 立方体の倍積問題 |  立方体の倍積問題 | 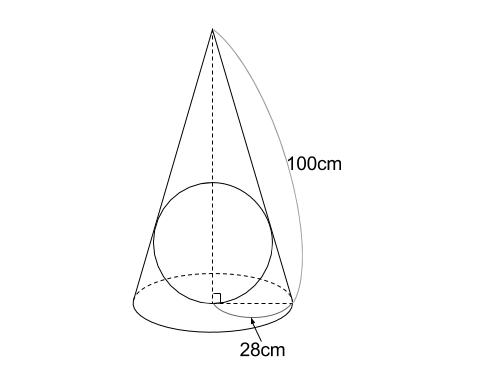 立方体の倍積問題 |
「円錐 問題 表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 立方体の倍積問題 |  立方体の倍積問題 |  立方体の倍積問題 |
 立方体の倍積問題 |  立方体の倍積問題 |  立方体の倍積問題 |
 立方体の倍積問題 |  立方体の倍積問題 | 立方体の倍積問題 |
「円錐 問題 表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 立方体の倍積問題 |  立方体の倍積問題 |  立方体の倍積問題 |
 立方体の倍積問題 |  立方体の倍積問題 |  立方体の倍積問題 |
 立方体の倍積問題 |  立方体の倍積問題 | 立方体の倍積問題 |
「円錐 問題 表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 立方体の倍積問題 |  立方体の倍積問題 |  立方体の倍積問題 |
 立方体の倍積問題 |  立方体の倍積問題 |  立方体の倍積問題 |
 立方体の倍積問題 | 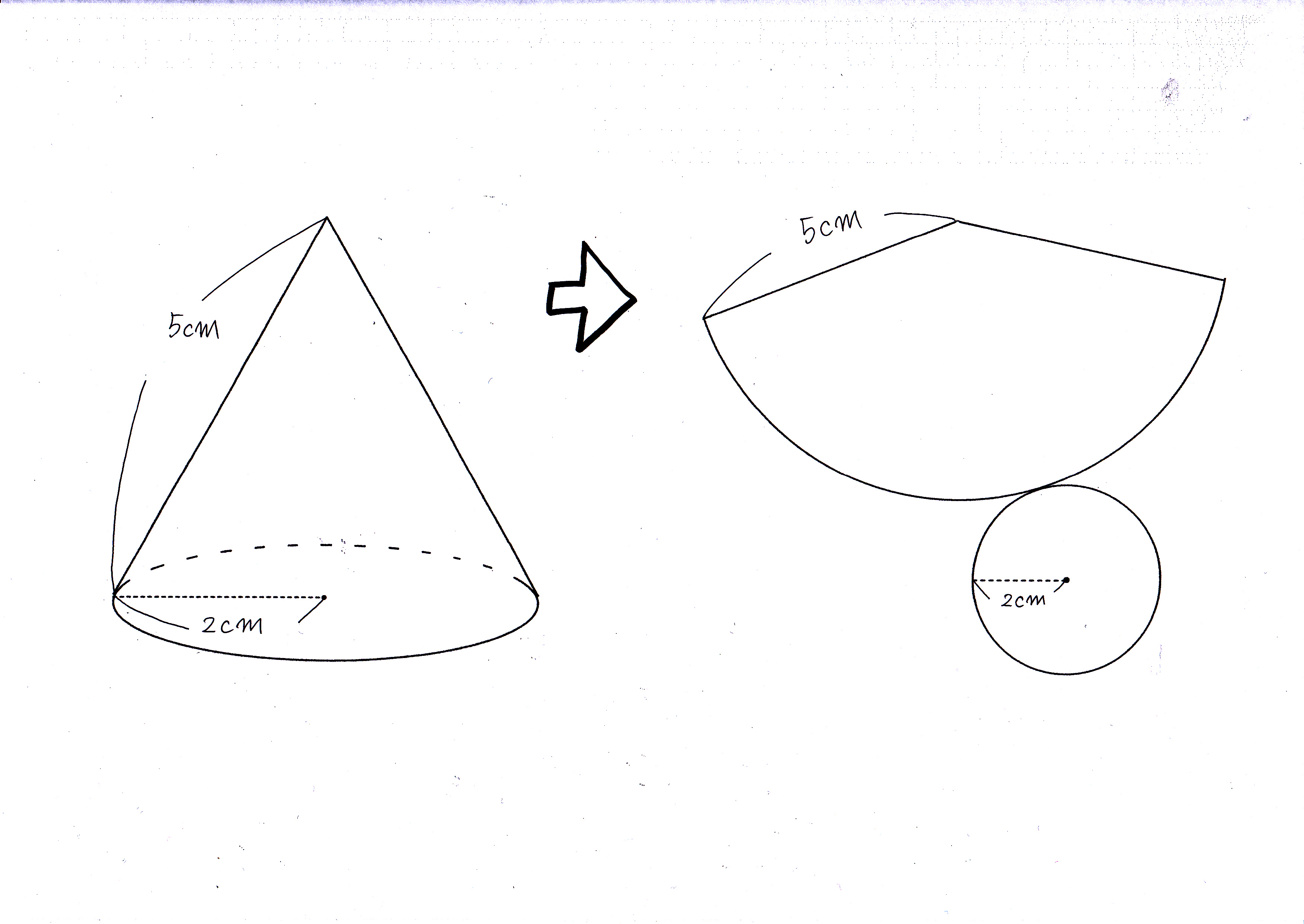 立方体の倍積問題 |  立方体の倍積問題 |
「円錐 問題 表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 立方体の倍積問題 |  立方体の倍積問題 |  立方体の倍積問題 |
 立方体の倍積問題 |  立方体の倍積問題 | 立方体の倍積問題 |
 立方体の倍積問題 |  立方体の倍積問題 |  立方体の倍積問題 |
「円錐 問題 表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 立方体の倍積問題 |  立方体の倍積問題 | 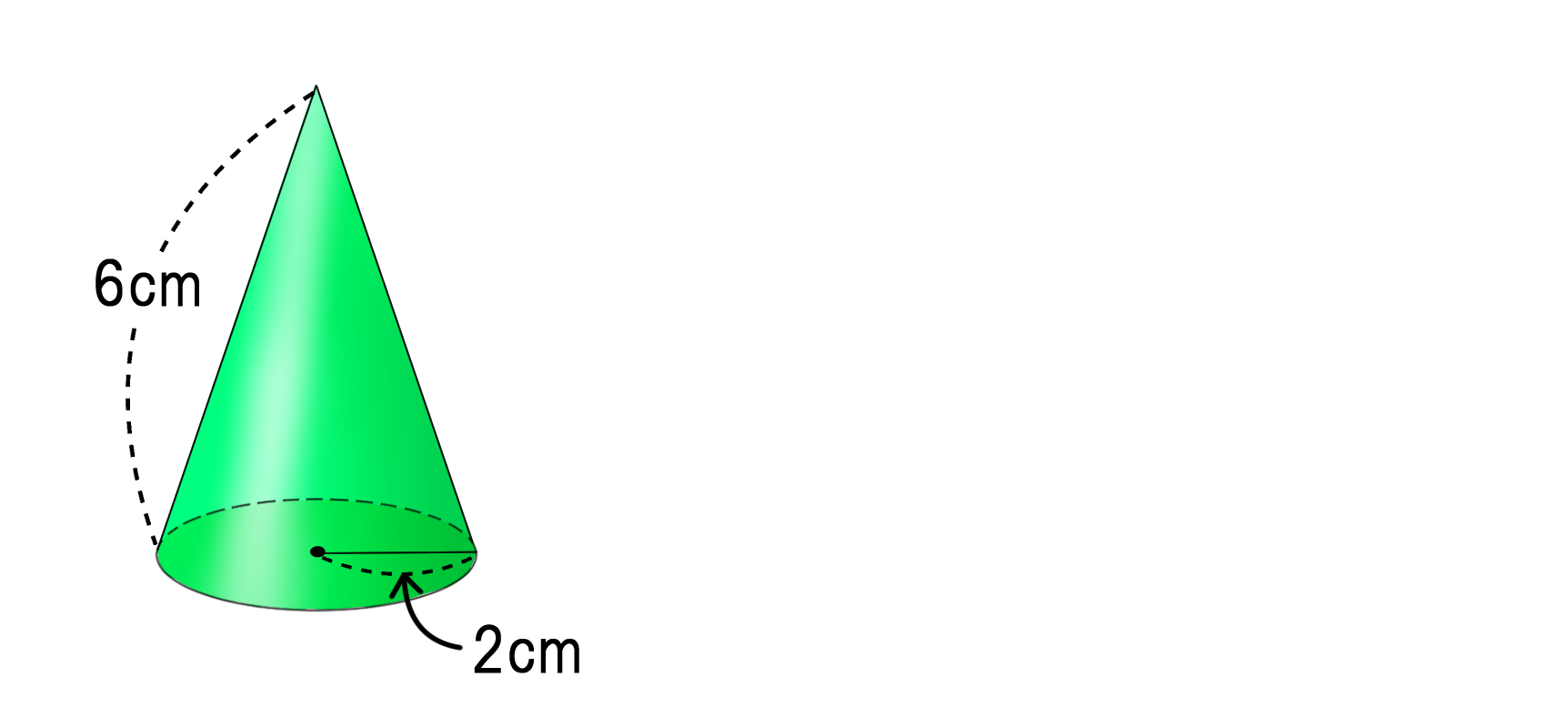 立方体の倍積問題 |
 立方体の倍積問題 |  立方体の倍積問題 |  立方体の倍積問題 |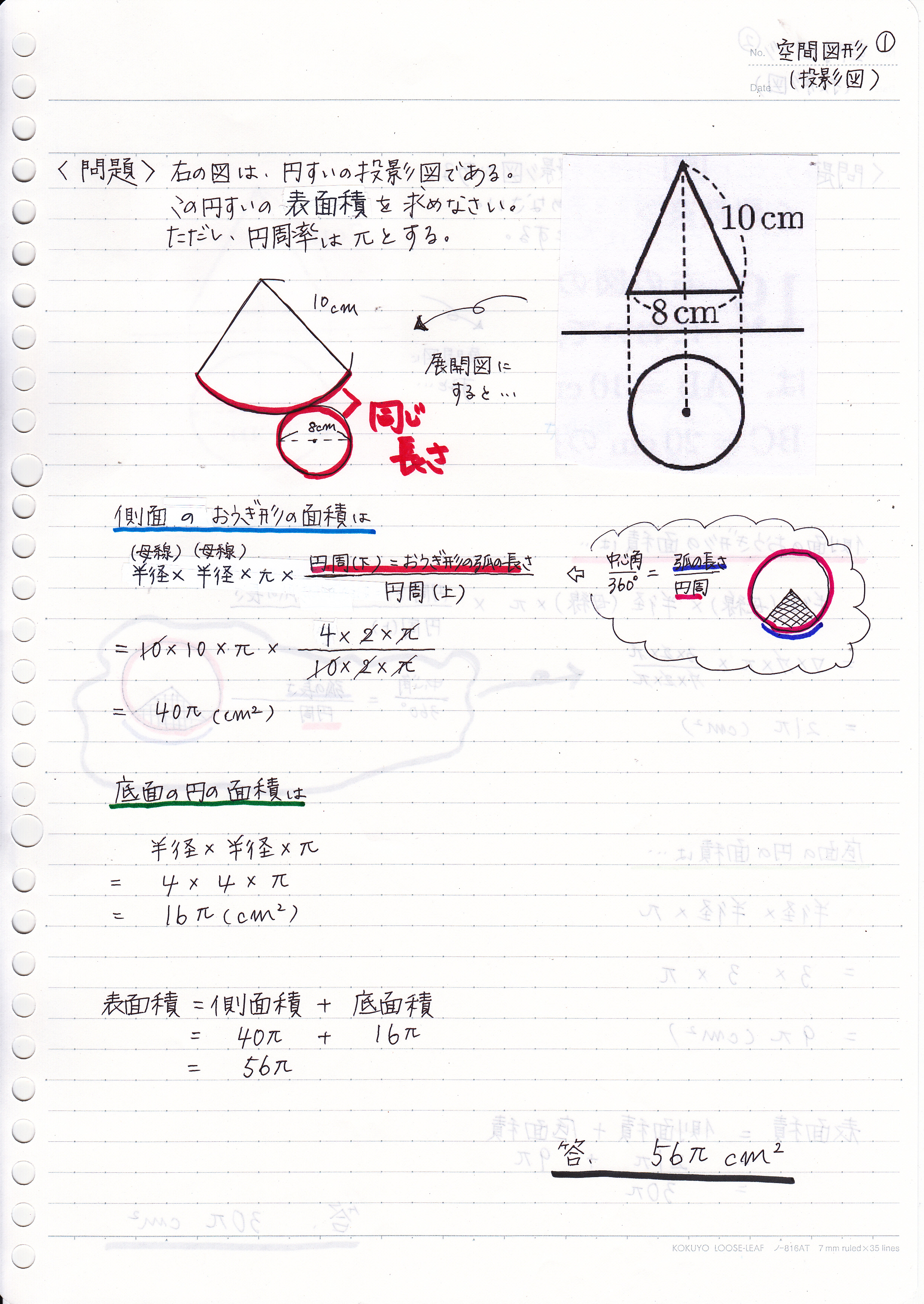
立方体の倍積問題 |  立方体の倍積問題 |  立方体の倍積問題 |
「円錐 問題 表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 立方体の倍積問題 |  立方体の倍積問題 | 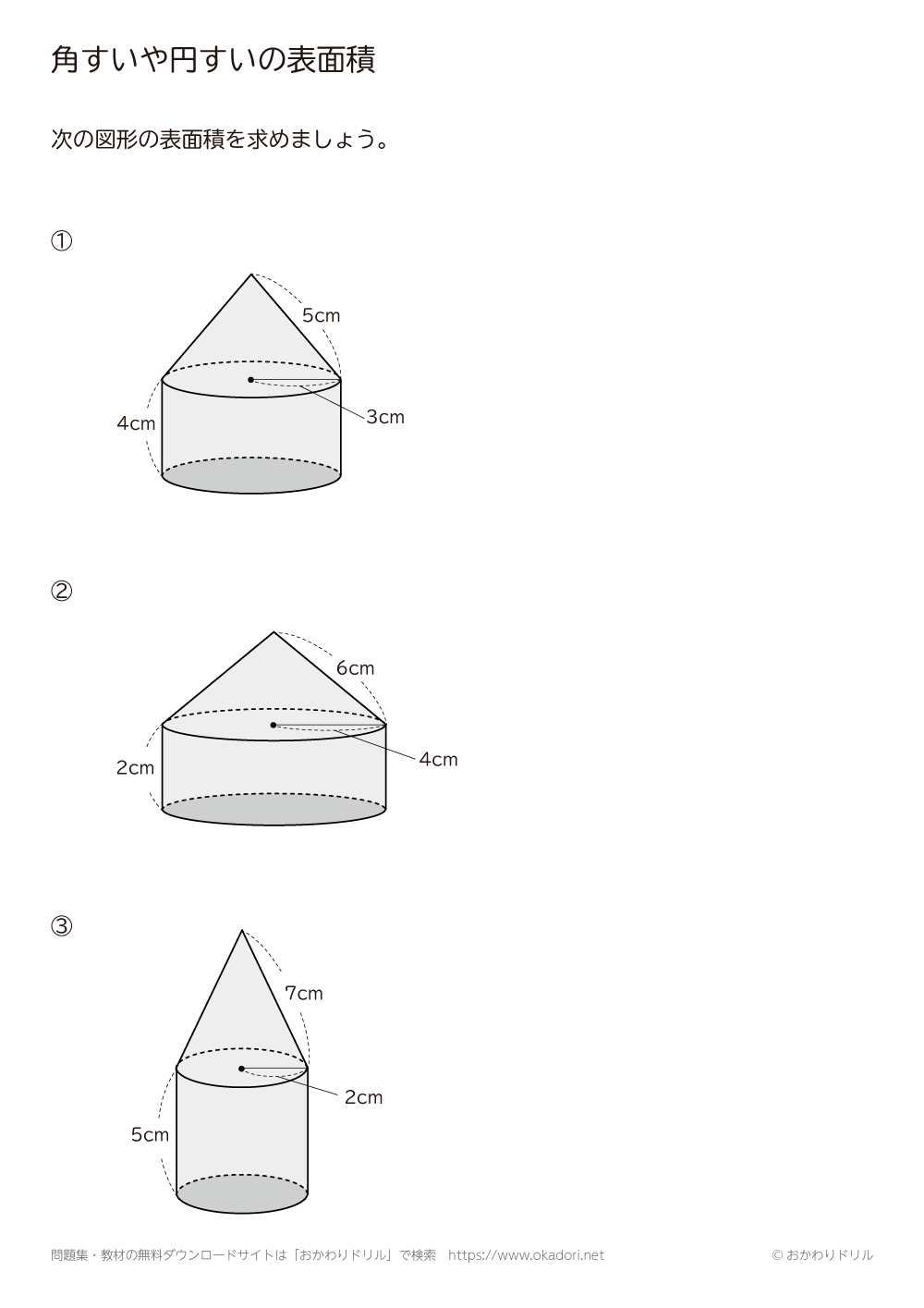 立方体の倍積問題 |
 立方体の倍積問題 |  立方体の倍積問題 |  立方体の倍積問題 |
 立方体の倍積問題 |  立方体の倍積問題 | 立方体の倍積問題 |
「円錐 問題 表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
立方体の倍積問題 |  立方体の倍積問題 |  立方体の倍積問題 |
 立方体の倍積問題 |  立方体の倍積問題 |  立方体の倍積問題 |
 立方体の倍積問題 |  立方体の倍積問題 |  立方体の倍積問題 |
「円錐 問題 表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 立方体の倍積問題 |  立方体の倍積問題 |  立方体の倍積問題 |
 立方体の倍積問題 |  立方体の倍積問題 |
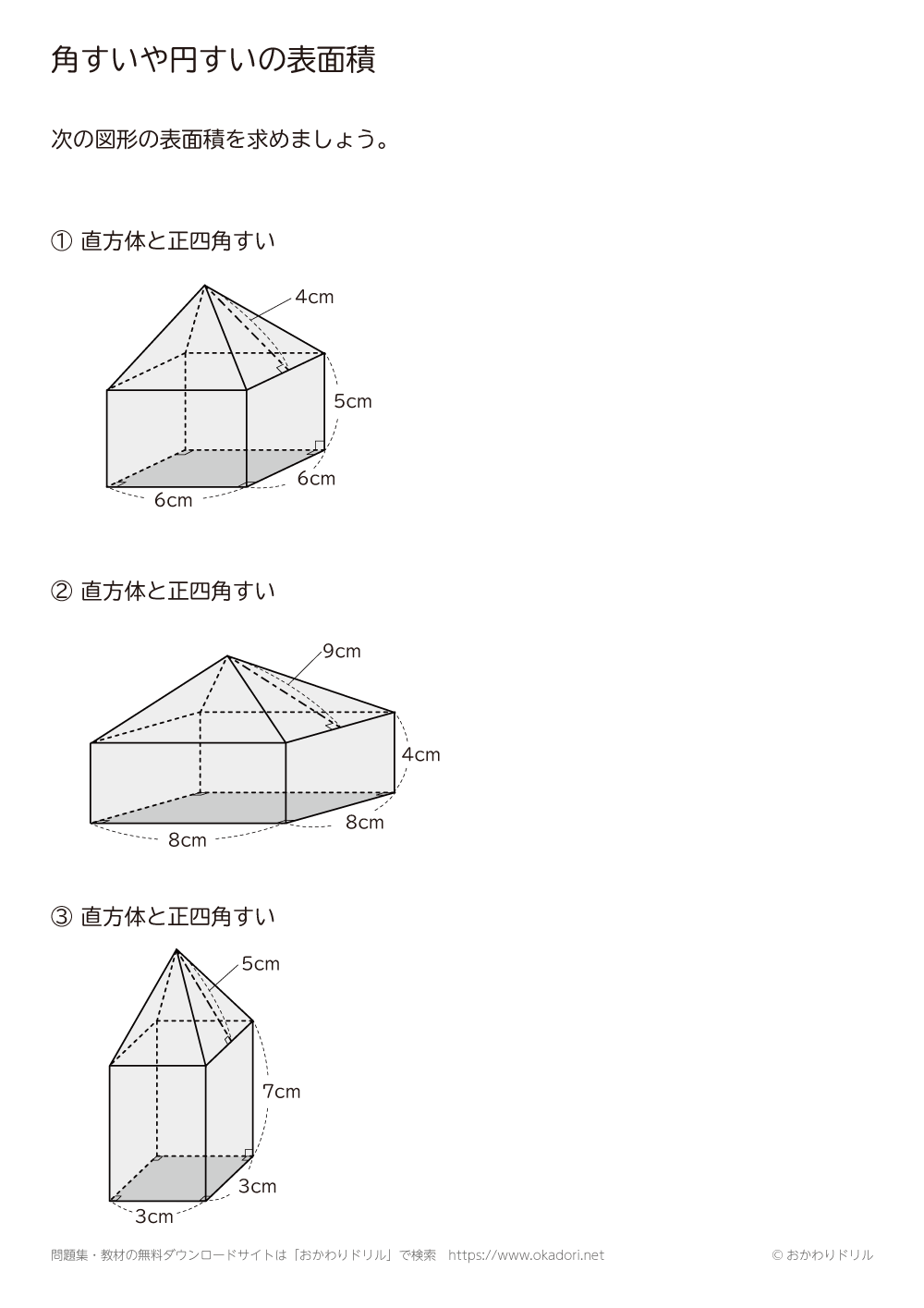
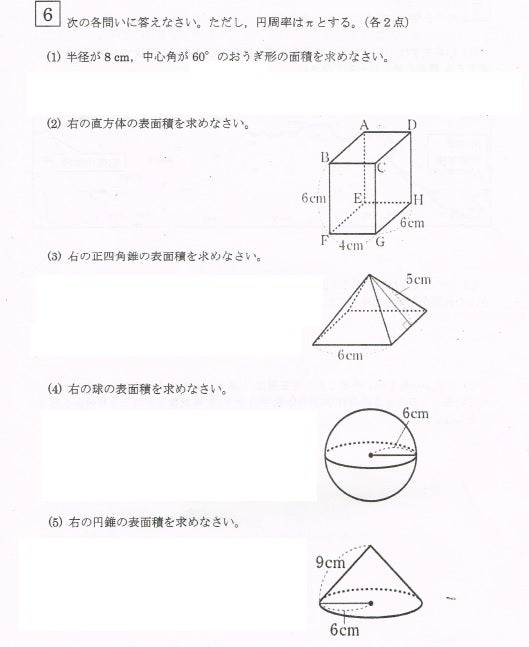
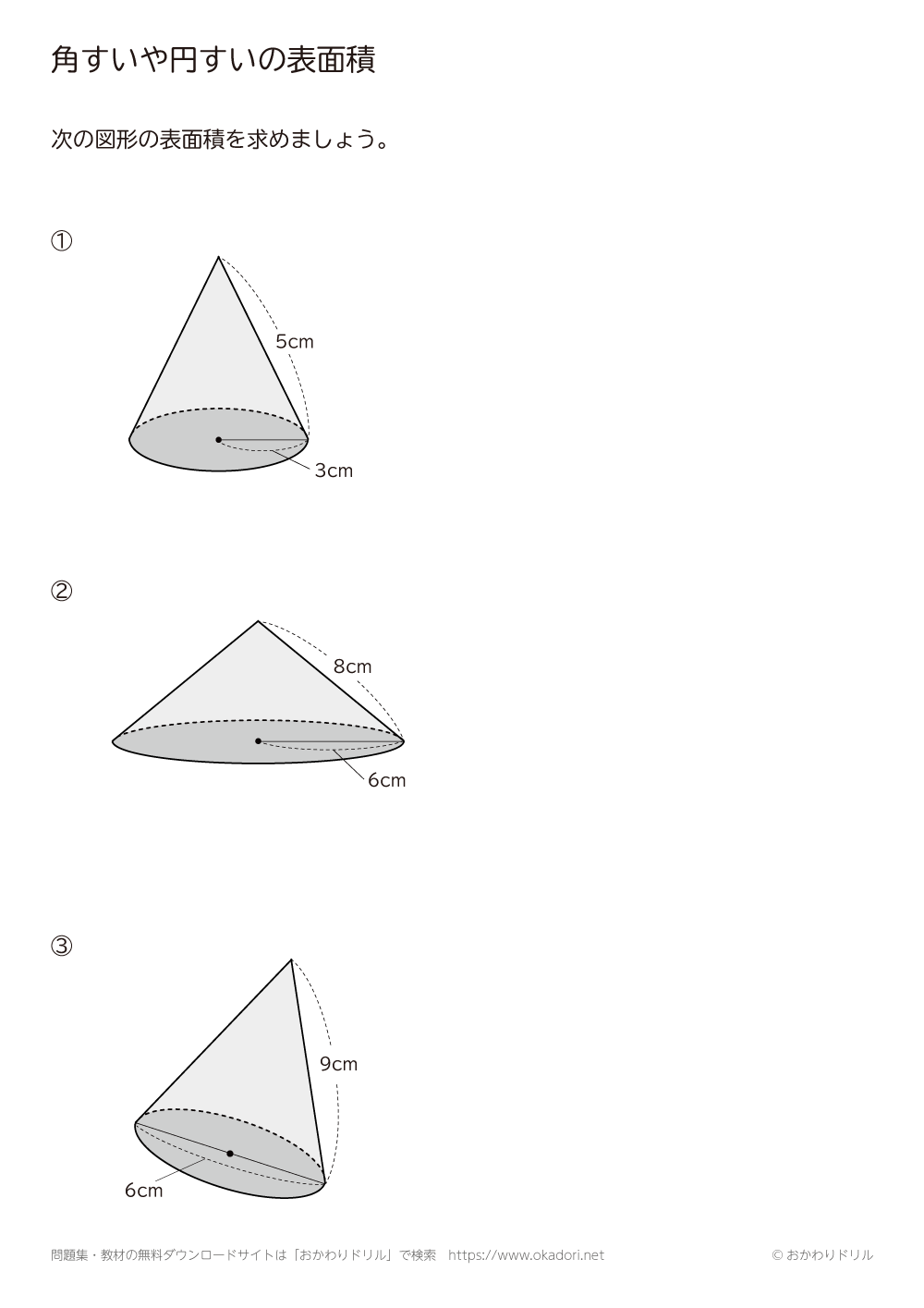
立体の表面積を求める問題です。 考え方のポイント 立体の表面積は展開図を書いて考えましょう。 例）立方体は正方形が6枚 正方形の面積×6 ＊展開図が頭に思い浮かぶ場合は直接求めて構いませんが、よく分からない場合は自分で展開図を書いて長さを書いていくようにしてください。円錐と内接球・その1 問題 下の図のように、底面の半径が 28cm 28 c m ,母線の長さが 100cm 100 c m の円錐に 球が内接しています。 この球の半径を求めなさい。 解説 平面における、「三角形と内接円の関係」とほぼ同じです。 空間図形においても、着目すべき「平面」で解きます。 どの平面に着目すべきか考えましょう。 もちろん下の図のような、三角形 P AB P A B に着目します。 AB A B は
Incoming Term: 円錐 問題, 円錐 問題集, 円錐 問題 中3, 円錐 問題 中学受験, 円錐 問題 表面積, 円錐 問題 最短距離, 空間図形 円錐 問題, 中1 数学 円錐 問題, 角錐 円錐 問題, 算数 円錐 問題,
0 件のコメント:
コメントを投稿