25 ++ 平行四辺形の面積の求め方 高校 342305-平行四辺形の面積の求め方 高校

平行四辺形と比 教遊者

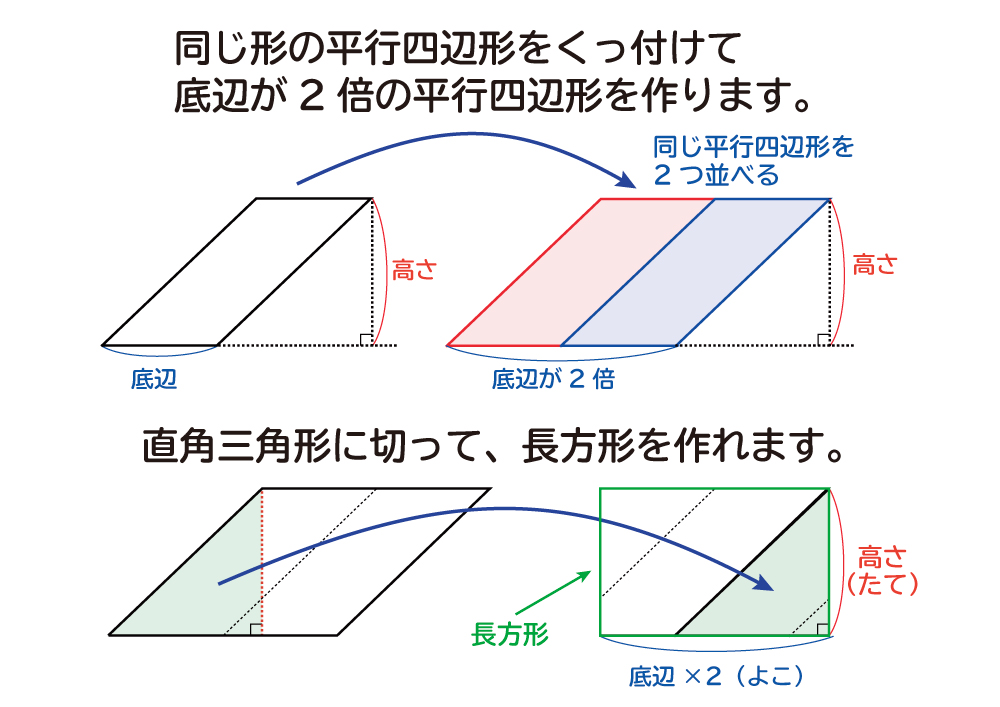
よって、求めたい平行四辺形の面積は abdを2倍したものになるので 答えは160㎠ となります。 このように、平行四辺形の中にある三角形を見つけながら 相似な図形から面積比を求めたり 高さが等しい三角形から面積比を求めたりします。向かい合う辺がそれぞれ平行の四角形を『 平行四辺形 （ へいこうしへんけい ） 』と言いますが、平行四辺形の面積は正方形や長方形同様、簡単な計算で求めることができます。 なぜ簡単な計算で求められるのか。それは図形を変形するだけなので、図を使って説明すれば小学生でもすぐに

平行四辺形の面積の求め方 高校

平行四辺形の面積の求め方 高校-数学切り抜き帳 このタイトルを見て「こんなこと誰でも知っているのに」と思う読者もいるに違いない， 確かに面積の求め方は誰でも知っている．しかし，この求め方（計算法）の根底にあるものを 高校生の目で 見直してもらいたい． 平行四辺形の (平行四辺形ABCD) = ABC = (平行四辺形ABCD) よって ABC = （証明おわり） 2 つぎに、数Ⅰ三角比から はさむ辺 はさむ辺 はさまれた角のサイン です。 記号で書くと3通りになりますが、ジュウゴは↑のようなイメージで教えています。 使う場面は 二辺とその間の角度がわかっている 三辺の長さがわかっている ときなどです。 使い方 例題2） , , の ABCの面積を求めよ。 ポイント

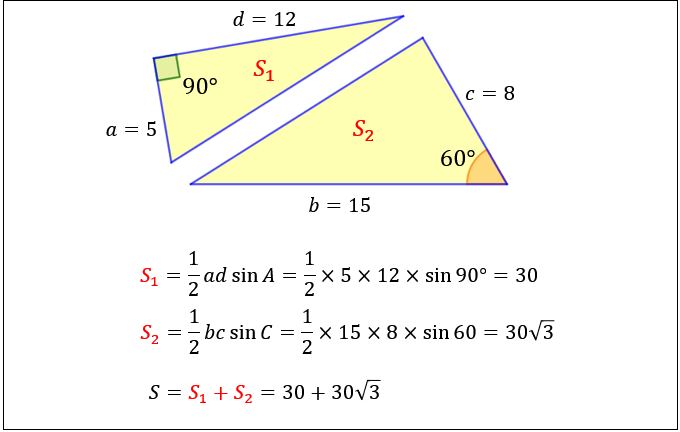
四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

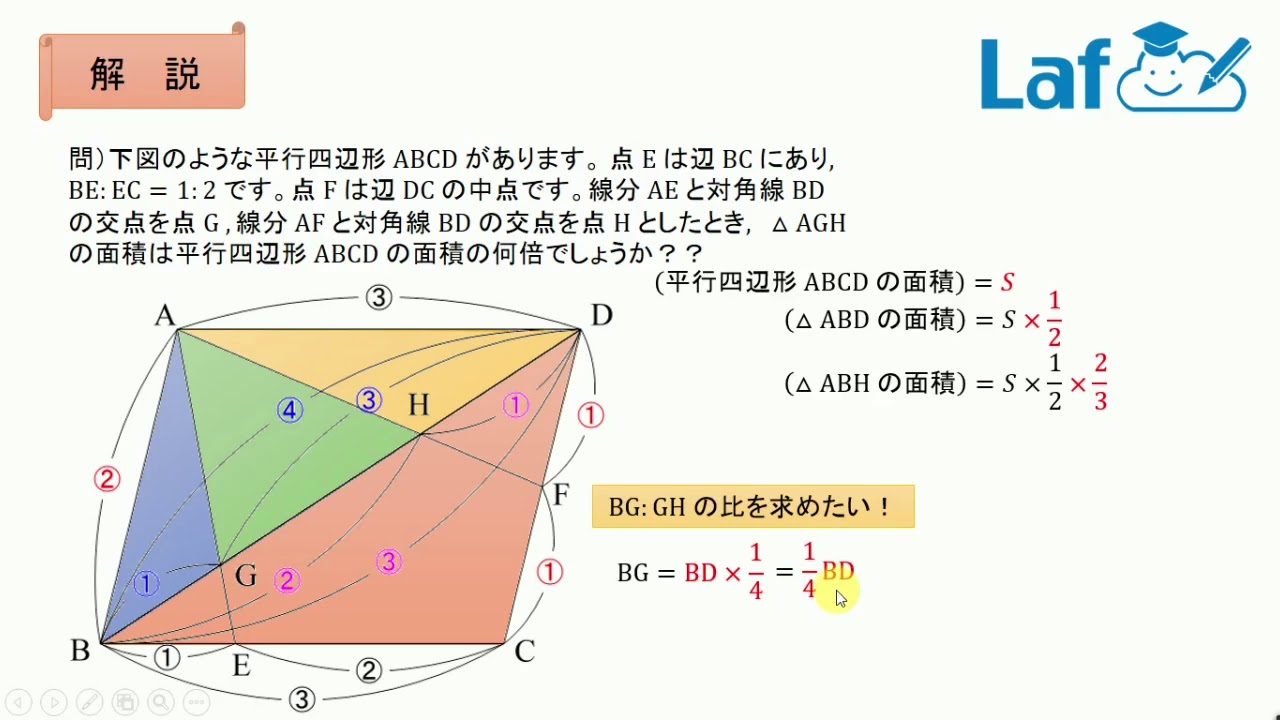
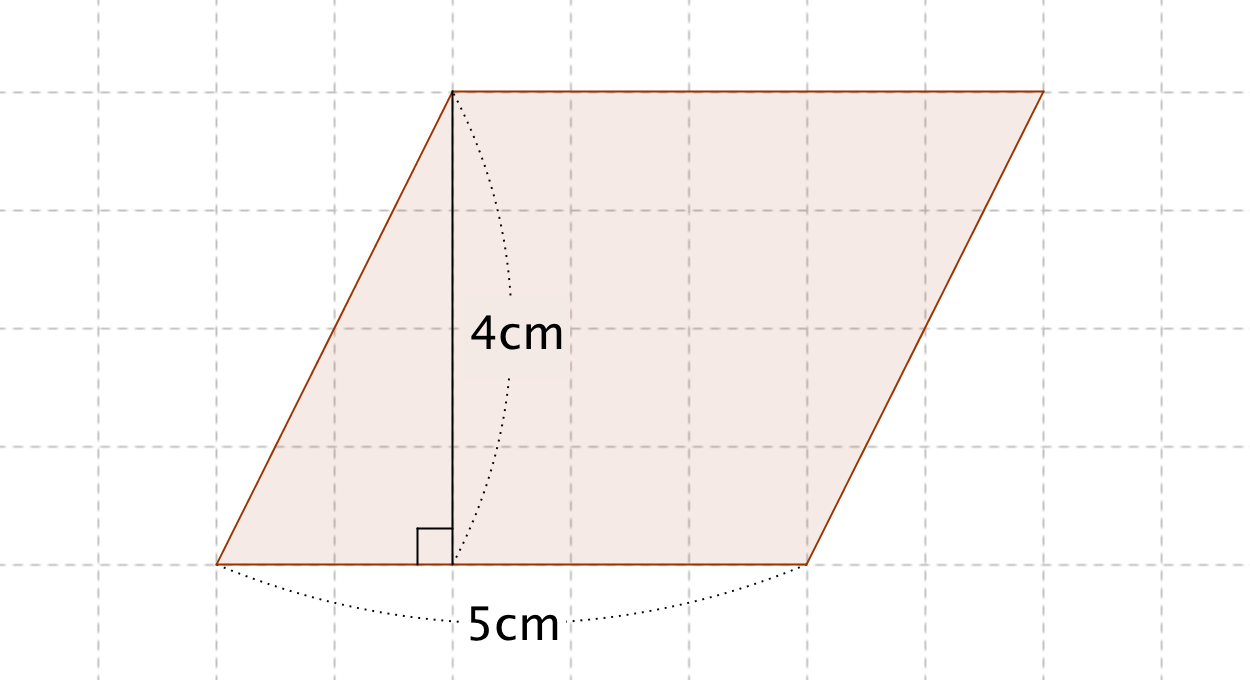
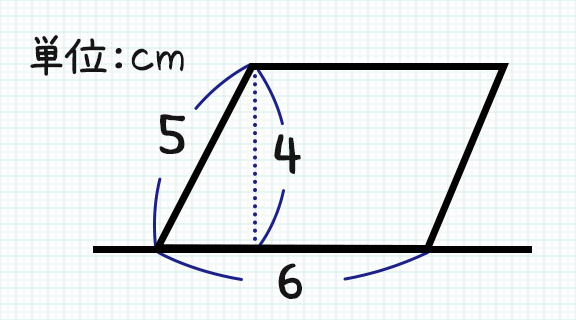
底辺の長さ $a$、高さ $h$ の平行四辺形の面積 $S$ は、次の公式で求められます。 平行四辺形 (へいこうしへんけい) の面積 \begin{align*} S = ah \end{align*} 面積 = 底辺 × 高さ 公式の 導出 (どうしゅつ) 方法と計算 例 (れい) は「平行四辺形の面積の求め方」をご覧ください。 aq cq 2 3であることから, 上の面積比の関係から, abqと cbqの面積比は, 基本パターンより, abq cbq ② ③。 このとき, pq bq 2 3と, abq ②を用いて, apqの面積の割合をもとめると, 基本パターンより, 2 3 apq ② apq となります。 ここで, 平行四辺形abcdの半分の面積は abcが⑤, ( ② ③ )であることから, adcも⑤, apq より, 四角形pqcd ⑤ よって, 求める面積比は, ⑤ 2 最後に平行四辺形の面積は対角線で区切った三角形 abdの2倍になります。 よって、30×2＝60で60㎠と答えが求まります。 まとめ この問題に慣れて頭の中ですらすら解いていけるようになるとめっちゃ面白いです。 すぐ飽きますけど。笑

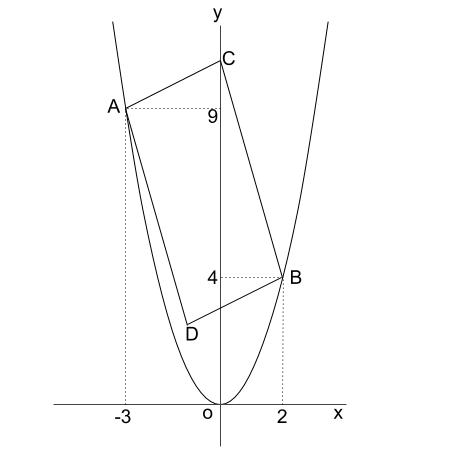
よって平行四辺形の面積は 21×2=42 解法2 直線ABとx軸の交点の座標をPとすると 平行四辺形の面積は (Pのx座標)×(Cのy座標)で求められる。 ここで点Pの座標は直線ABがy=3x14であるから (14/3、0)だと求められる。 よって 14/3×9=42 解法3 tum******** さん /7/6 1038 ベクトル記号を省きます。 A・B=343=10 A=B=√14 ∠AOB＝θとおく cosθ=10/√14・√14=5/7 sin^2θ=1cos^2θより sinθ=2√6/7 平行四辺形の面積S S= OAB×2=√14・√14sinθ =14・ (2√6/7) =4√6 あわせて知りたい この問題で、原点Oを通り、平行四辺形の面積を2等分する直線の式の求め方と答えを教えてください ♀️ 三角形はなん正方形の面積 長方形の面積 台形の面積 台形の高さ・面積（4辺の長さから） 台形の1辺・面積（3辺の長さと高さから） ひし形の面積 平行四辺形の面積（底辺と高さから） 平行四辺形の面積（2辺と夾角から） 円に内接する四角形の面積（4辺から） 四角形の面積（4辺と対角の和から） 正多角形の面積

平行四辺形の面積の求め方 高校のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

平行四辺形を分ける面積比の求め方 算数解法の極意	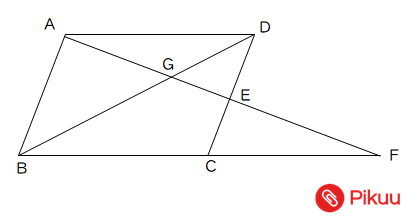平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	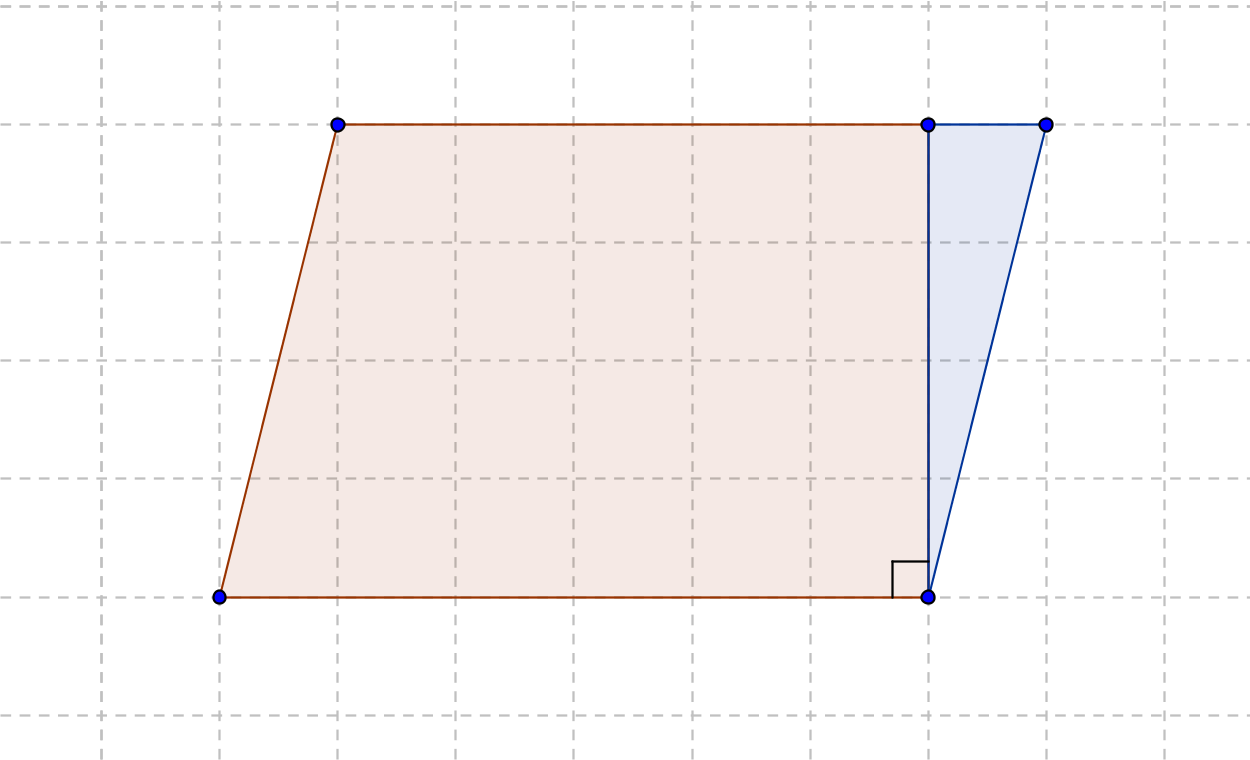平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意	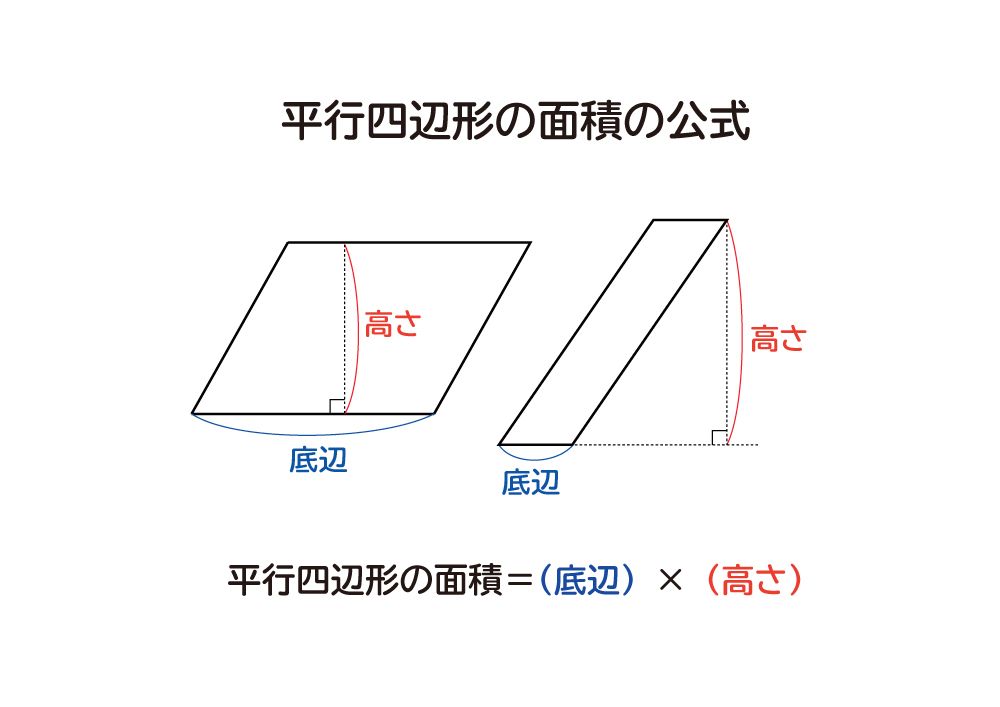平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意	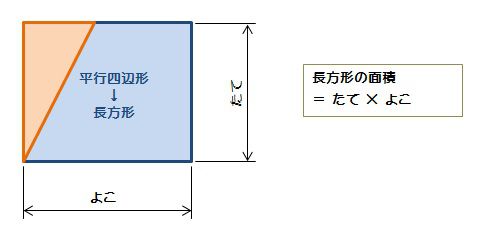平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意	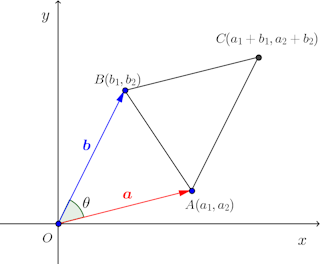平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	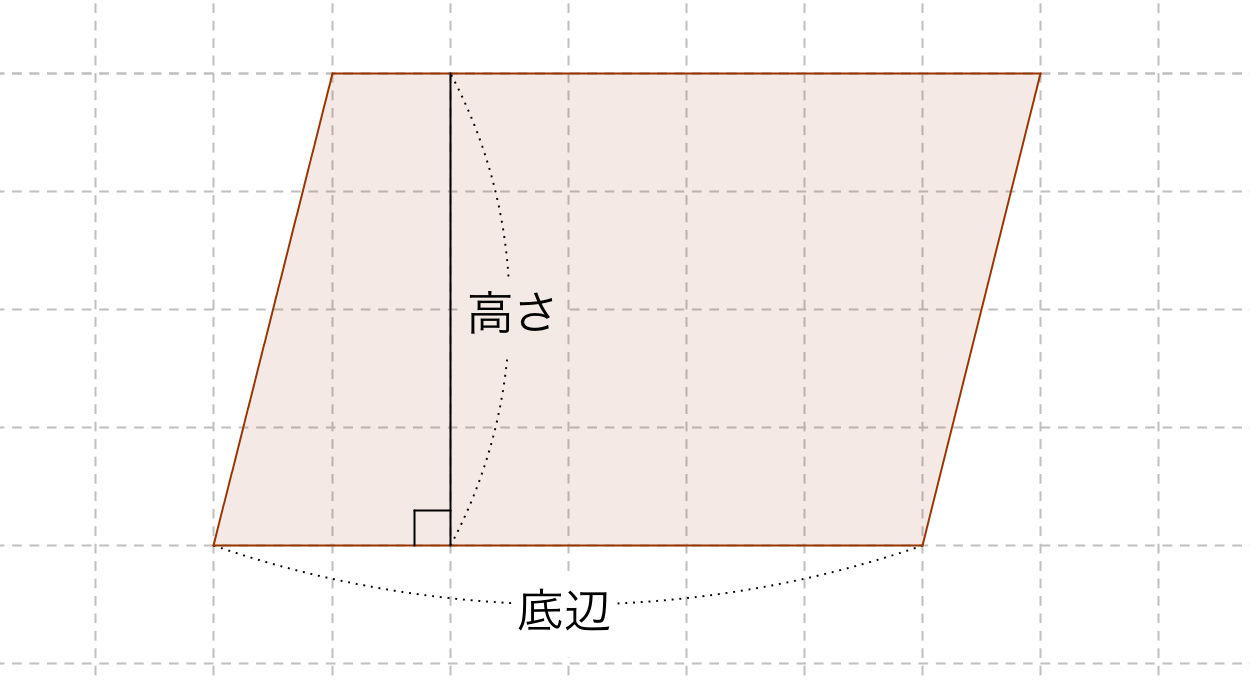平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意	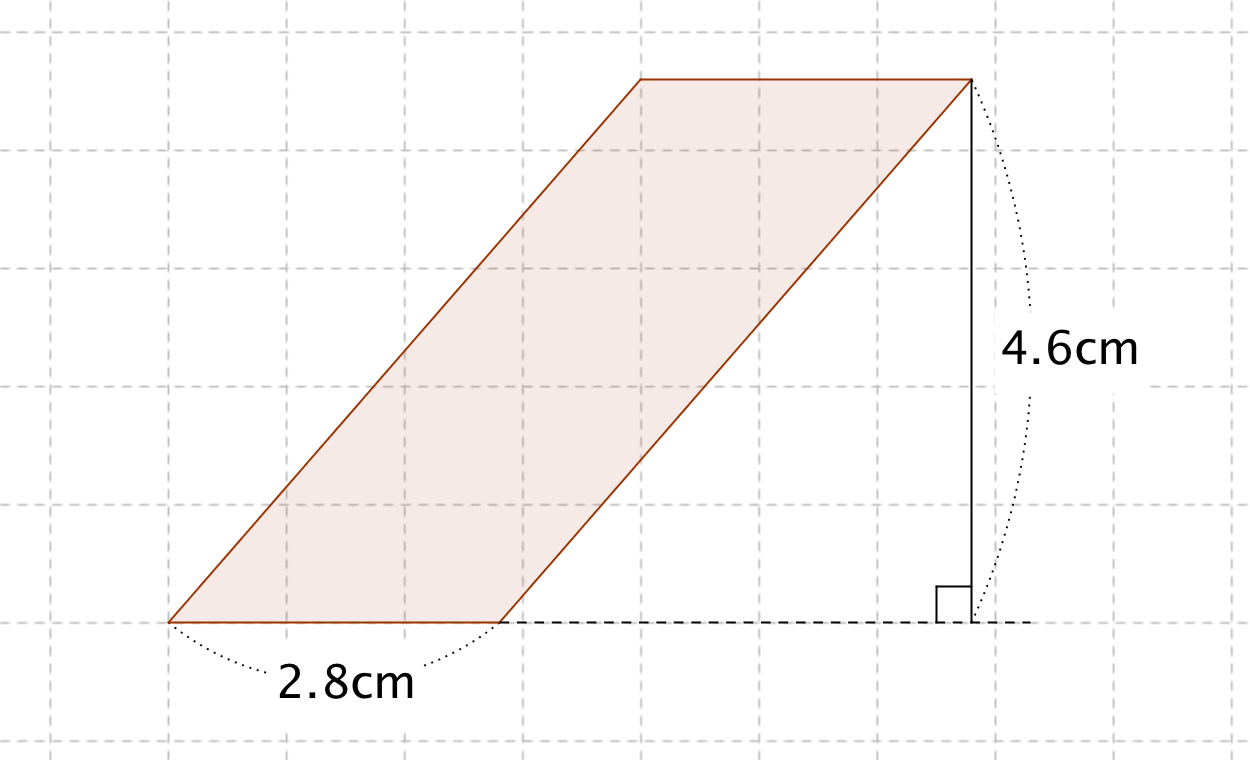平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	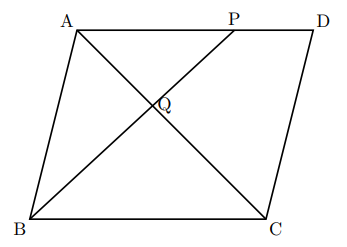平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	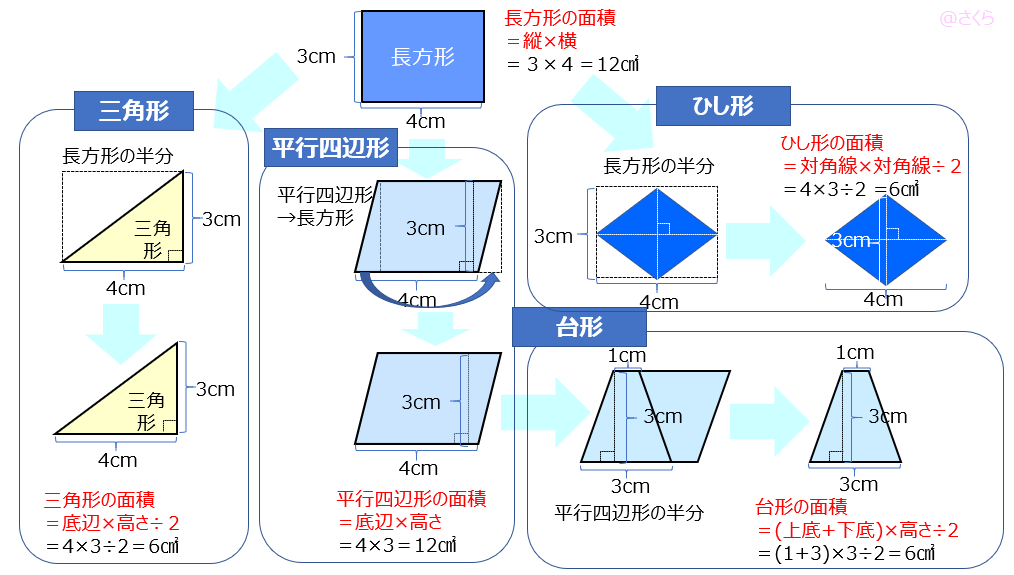平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	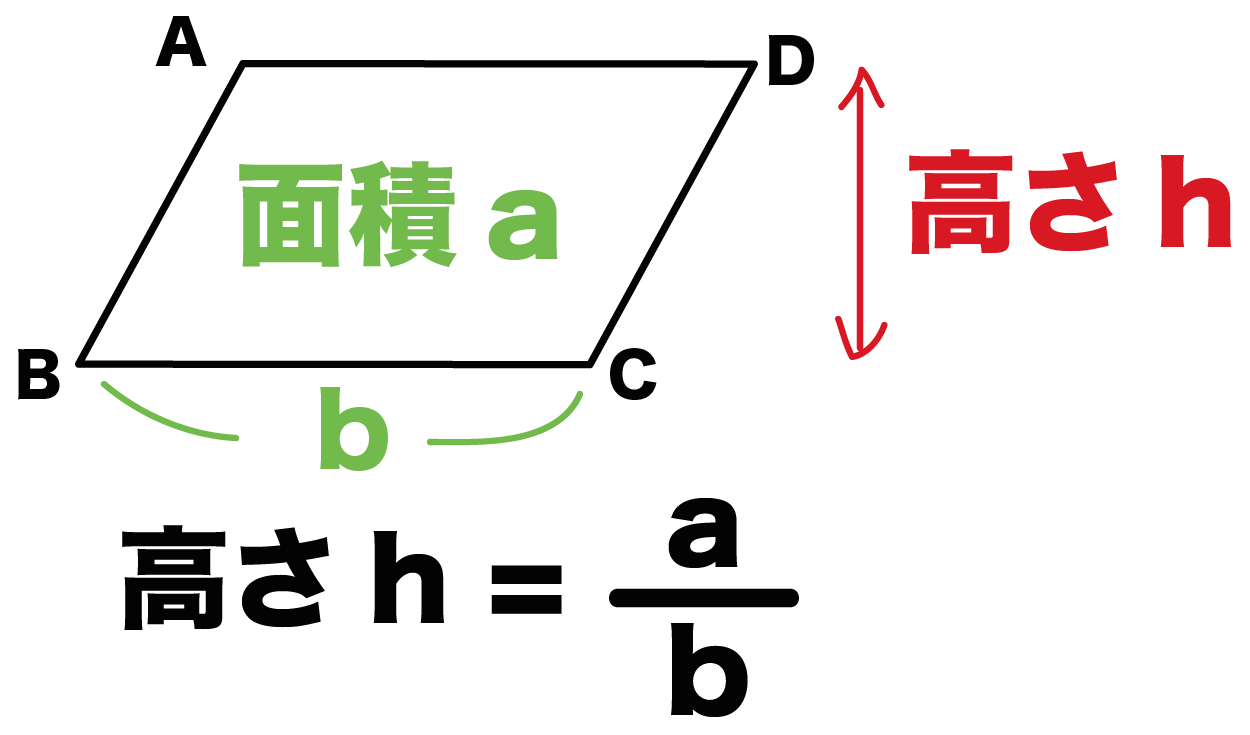平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	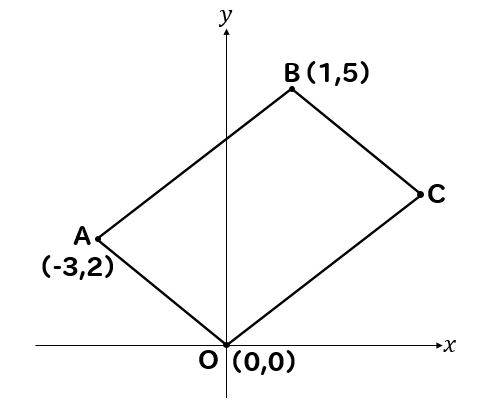平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	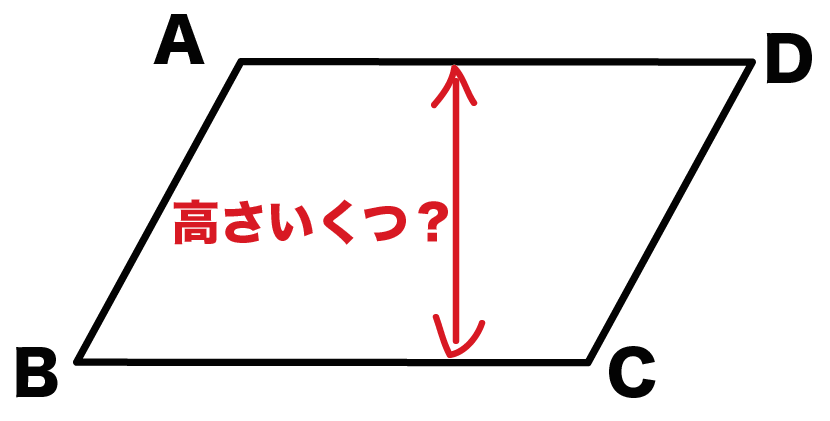平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	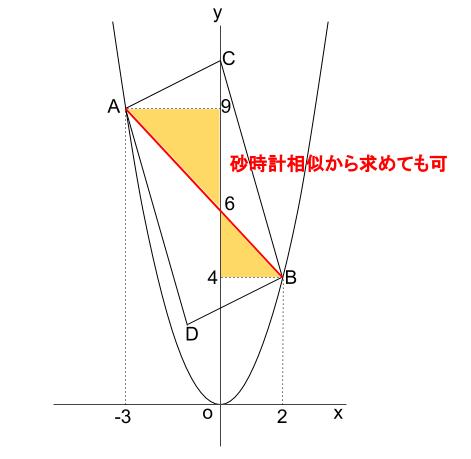平行四辺形を分ける面積比の求め方 算数解法の極意	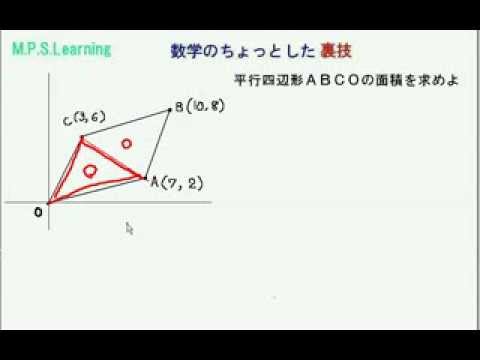平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意	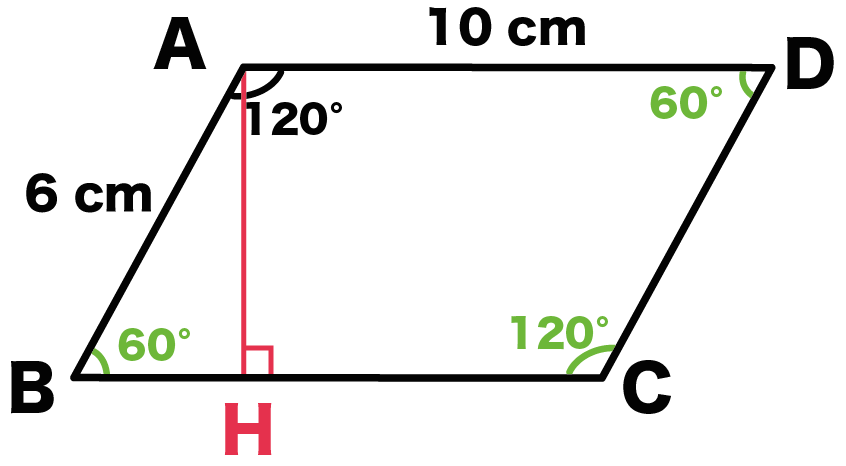平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	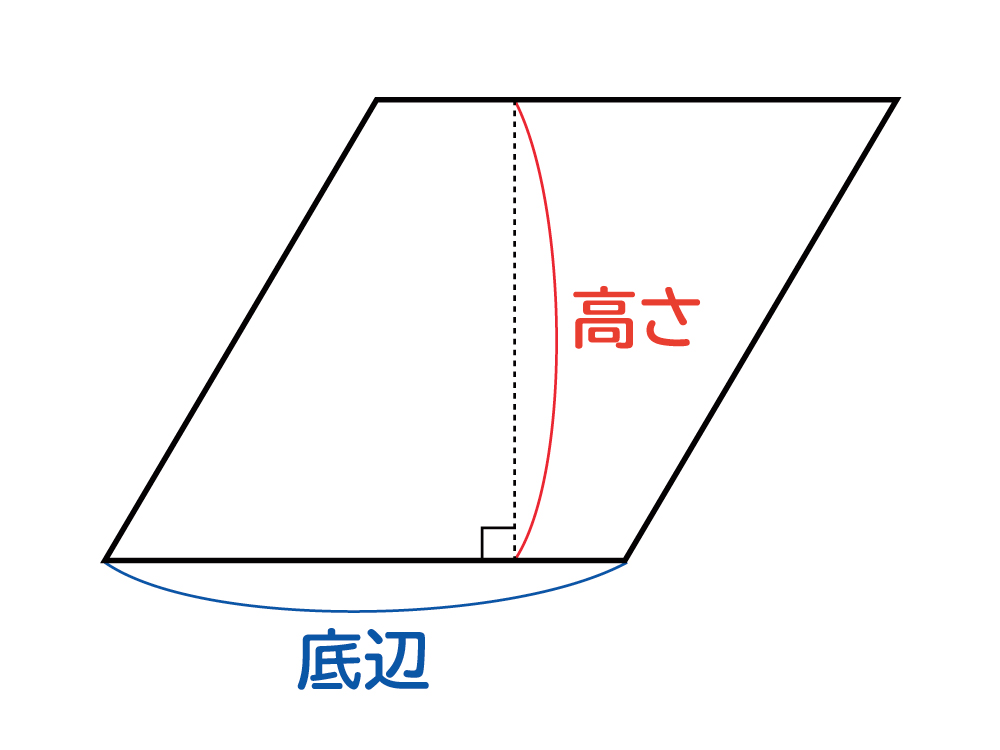平行四辺形を分ける面積比の求め方 算数解法の極意	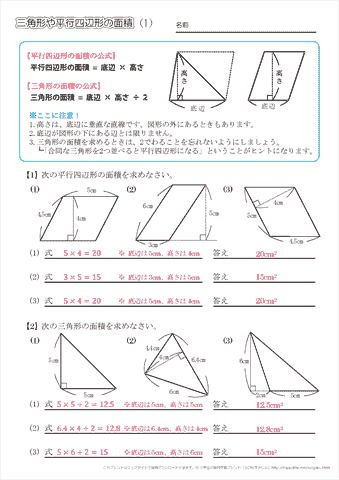平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	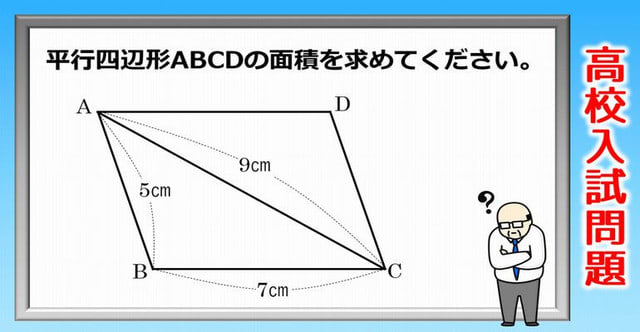平行四辺形を分ける面積比の求め方 算数解法の極意	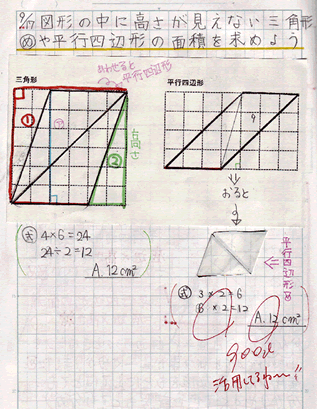平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意	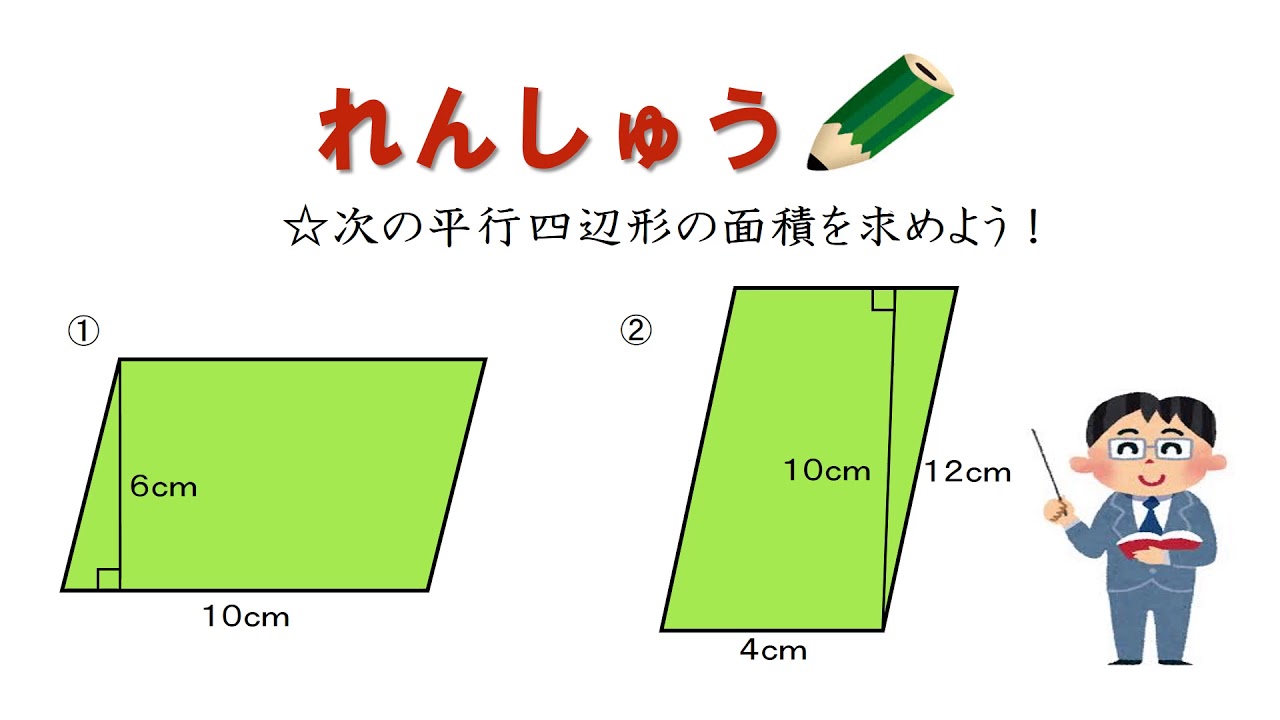平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意
平行四辺形を分ける面積比の求め方 算数解法の極意	平行四辺形を分ける面積比の求め方 算数解法の極意

 myz******** myz******** さん 12/1/1 1656 1 1 回答 行列式を使った、面積の求め方 行列式を使った、面積の求め方 図の平行四辺形の面積が a c abs b d ＝abs（adbc） となるみたいです これは、どのように考えているのでしょうか 高校で習ったらしいのですがまったく思い出せません； ちなみに、absは絶対値の意味です 高校数学 ・ 1,126 閲覧 ・ xmlns="http//wwww3次の図のような平行四辺形abcdについて考える。 線分bdはこの平行四辺形の対角線であり∠abcの角の二等分線である。 また、点eは線分bcの中点である。 このとき 面積比 abf： bef： afd：四角形cdfe について求めよ。

Incoming Term: 平行四辺形の面積の求め方 高校,